Quantum processes of inherent dynamical nature, such as quantum walks, defy a description
in terms of an equilibrium statistical physics ensemble. Until now, identifying the general
principles behind the underlying unitary quantum dynamics has remained a key challenge. Here,
we show and experimentally observe that split-step quantum walks admit a characterization
in terms of a dynamical topological order parameter (DTOP). This integer-quantized DTOP
measures, at a given time, the winding of the geometric phase accumulated by the wavefunction
during a quantum walk. We observe distinct dynamical regimes in our experimentally realized
quantum walks, and each regime can be attributed to a qualitatively different temporal behavior
of the DTOP. Upon identifying an equivalent many-body problem, we reveal an intriguing
connection between the nonanalytic changes of the DTOP in quantum walks and the occurrence
of dynamical quantum phase transitions.
Light: Science &
Applications 9, 7 (2020)
Quantum information
Quantum information
Concepts from quantum information science have developed into central tools for quantum many-body theory. For example, exotic quantum phases such as spin liquids, topological, or many-body localized systems find their characterization in their peculiar quantum entanglement properties. Furthermore, entanglement plays a key role in many numerical approaches such as tensor network methods, which are developed at our institute. As such, entanglement in quantum many-body systems is not only important for the characterization of phases and phase transitions but also for the performance of computational approaches to describe such systems.
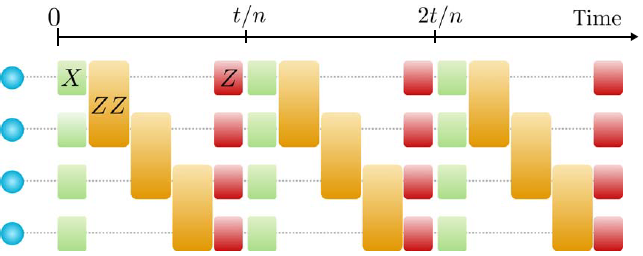
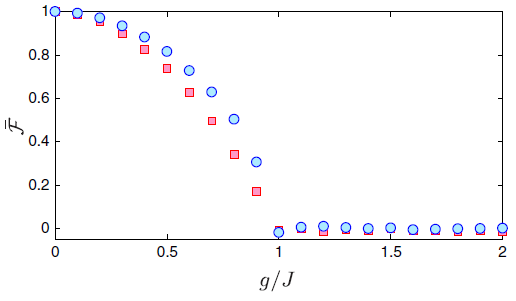
From the reverse perspective, quantum technological systems such as quantum computers are now on the way to reach a regime where quantum many-body effects start to play a crucial role. In this way, these experimental platforms constitute a natural interface between quantum information science and quantum many-body theory, where the knowledge of the properties of quantum many-body systems can be used to study quantum technological applications.
It is our purpose to explore the rich physics at this interface with the aim to improve computational methods such as tensor networks, to apply quantum information concepts such as entanglement to quantum many-body systems, or to use concepts from quantum many-body theory for a description of quantum technological applications. For more details on current and recent research highlights in this field see the collection below.
Quantum localization bounds Trotter errors in digital quantum
simulation
Markus Heyl, Philipp Hauke, and Peter Zoller
A fundamental challenge in digital quantum simulation (DQS) is the control of an inherent
error, which appears when discretizing the time evolution of a quantum many-body system as
a sequence of quantum gates, called Trotterization. Here, we show that quantum localization-
by constraining the time evolution through quantum interference-strongly bounds these errors
for local observables, leading to an error independent of system size and simulation time. DQS
is thus intrinsically much more robust than suggested by known error bounds on the global
many-body wave function. This robustness is characterized by a sharp threshold as a function
of the Trotter step size, which separates a localized region with controllable Trotter errors from
a quantum chaotic regime. Our findings show that DQS with comparatively large Trotter steps
can retain controlled errors for local observables. It is thus possible to reduce the number of gate
operations required to represent the desired time evolution faithfully.
Sci. Adv. 5, eaau8342 (2019)
Sci. Adv. 5, eaau8342 (2019)
Detecting Equilibrium and Dynamical Quantum Phase Transitions in Ising
Chains via Out-of-Time-Ordered Correlators
Markus Heyl, Frank Pollmann, and Balázs Dóra
Out-of-time-ordered (OTO) correlators have developed into a central concept quantifying
quantum information transport, information scrambling, and quantum chaos. In this Letter,
we show that such an OTO correlator can also be used to dynamically detect equilibrium as
well as nonequilibrium phase transitions in Ising chains. We study OTO correlators of an order
parameter both in equilibrium and after a quantum quench for different variants of transverse-
field Ising models in one dimension, including the integrable one as well as nonintegrable and
long-range extensions. We find for all the studied models that the OTO correlator in ground
states detects the quantum phase transition. After a quantum quench from a fully polarized
state, we observe numerically for the short-range models that the asymptotic long-time value of
the OTO correlator signals still the equilibrium critical points and ordered phases. For the long-
range extension, the OTO correlator instead determines a dynamical quantum phase transition in
the model. We discuss how our findings can be observed in current experiments of trapped ions
or Rydberg atoms.
Phys. Rev. Lett. 121, 016801 (2018)
Phys. Rev. Lett. 121, 016801 (2018)