Highlights
Publication Highlights
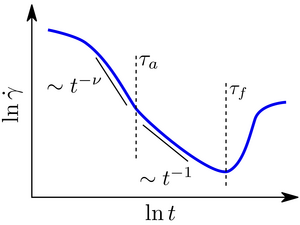
Scaling Description of Creep Flow in Amorphous Solids
Amorphous solids, which include colloidal glasses, dense emulsions, foams, and granular materials, are ubiquitous and important in both engineering and industry. When subjected to a suddenly imposed stress, they can exhibit a transient flow known as creep during which the flow rate decays as a power law over time. This power law is characterized by a quantity called the creep exponent. If the stress inducing the creep flow is low, the material eventually stops moving. But if this stress is sufficiently high, the power-law decay can be followed by sudden fluidization. Together with colleagues from École polytechnique fédérale de Lausanne (EPFL) and Université Paris-Saclay, Marko Popović of the Max Planck Institute for Physics of Complex Systems developed a theory of creep flow that can predict both the creep exponent and the time at which sudden fluidization occurs, as well as the temperature dependence of these two quantities. These predictions have been tested in numerical simulations and are consistent with previously published experimental observations. The key ingredient of the proposed theory is the new concept of a transient yield stress, which reflects the dynamics of the maximal stress that the material could sustain without flowing while it undergoes creep flow. Remarkably, the scaling of the creep exponent and the time of fluidization then follow from generic properties of the transient yield stress for both athermal and thermal systems. The success of the transient yield stress concept opens new exciting questions: What is the origin of the transient yield stress and what controls its dynamics? Can the concept of a transient yield stress be employed to describe other characteristic behaviours associated with the yielding of amorphous solids, such as shear banding instabilities?
Marko Popović, et al., Phys. Rev. Lett. 129, 208001 (2022), Editors' Suggestion
Selected for a Synopsis in Physics
weiterlesenMarko Popović, et al., Phys. Rev. Lett. 129, 208001 (2022), Editors' Suggestion
Selected for a Synopsis in Physics
Publication Highlights
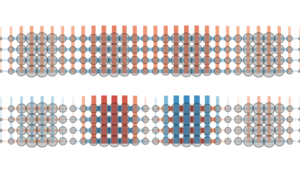
Fragmented Cooper Pair Condensation in Striped Superconductors
The mechanism behind high-temperature superconductors has long been a great mystery to physicists. Even though the fundamental physical equations of interacting electrons in these materials are well-known, their solution has proved challenging. Whether or not superconductivity or the so-called "stripe order", where the density of electrons forms regular waves called "stripes", is realized has been an open question and these two states of matter have been considered in competition to one another.
This study now shows that stripe order and superconductivity can, in fact, get along with one another quite well. By performing exact numerical simulations on a minimal model for cuprate superconductors, the author demonstrates that there exist states of matter with exactly one superconducting condensate per stripe. Since there are multiple stripes in the systems, there are also multiple condensates, a phenomenon called "fragmentation". The physical picture proposed in this study agrees well with experimental observations and demonstrates the predictive power of modern numerical techniques to study quantum many-body systems.
A. Wietek, Phys. Rev. Lett. 129, 177001 (2022)
weiterlesenA. Wietek, Phys. Rev. Lett. 129, 177001 (2022)
Publication Highlights
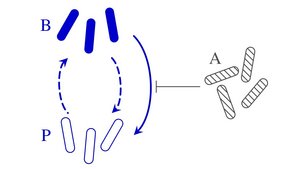
Responsive switching between subpopulations can stabilise microbial communities
The different microbial species in complex ecological communities like the human microbiome often have different subpopulations called phenotypes, between which they can switch stochastically or in response to environmental cues, such as toxins released by competitors or antibiotics. Pierre Haas of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute of Molecular Cell Biology and Genetics and collaborators at the University of Cambridge have analysed the ecological implications of such responsive switching. They combined a statistical analysis of many-species systems, a numerical study of a minimal two-species model, and analytical results for still simpler mathematical models. While responsive switching to a rare phenotype is destabilising on average, they could show that responsive switching to a rare "attack" phenotype is stabilising on average. A similar "attack" subpopulation was recently observed experimentally, which underlines the importance of responsive switching for ecological stability.
P. A. Haas, M. A. Gutierrez, N. M. Oliveira, and R. E. Goldstein, Phys. Rev. Research 4, 033224 (2022)
weiterlesenP. A. Haas, M. A. Gutierrez, N. M. Oliveira, and R. E. Goldstein, Phys. Rev. Research 4, 033224 (2022)
Publication Highlights
The rise to royalty; how paper wasps balance specialization and plasticity
Biological systems fascinate scientists across disciplines because of the highly complex structures that emerge from these systems, from cells to organisms and societies. While biological systems fulfil highly specialised tasks despite noisy signals, they can also rapidly break up these structures and perform entirely different tasks when the right signals are present. A new study in Cell Systems published by Adolfo Alsina and Steffen Rulands from MPI-PKS, Wolf Reik from the Babraham Institute in Cambridge and Solenn Patalano from the BBSRC Alexander Fleming in Athens used paper wasps as a paradigmatic example.
Paper wasps are social insects that display societal division of labor between workers and a queen. While this division of labor remains stable for the entire lifetime of the queen, when the queen is removed from the nest or dies the remaining workers can rapidly change their behavior and establish a new queen. Due to this behavior the paper wasps serve an experimental testing ground to study biological plasticity.
Rulands and colleagues carried out a unique set of experiments in Panama where they removed the queen from paper wasp nests and then followed the reorganization process back to the intact society simultaneously on different scales of biological organization: from time-resolved profiling of brains using multi-omics of the brains to colony-level video recordings. Using theory, they showed that by balancing antagonistic molecular and colony-level processes these societies are able to distinguish between different kinds of perturbations affecting the nest: intrinsic perturbations, such as molecular noise, affect insects independently of each other and these perturbations are actively suppressed by the society. By contrast, extrinsic perturbations affect the entire society and the society reacts plasticly. Given the above, the authors conclude that by employing a self-organised multi-scale mechanism Polistes manages to overcome the seeming paradox between specialisation and plasticity.
S. Patalano et al., Cell Systems 13, 1–12 (2022)
weiterlesenPaper wasps are social insects that display societal division of labor between workers and a queen. While this division of labor remains stable for the entire lifetime of the queen, when the queen is removed from the nest or dies the remaining workers can rapidly change their behavior and establish a new queen. Due to this behavior the paper wasps serve an experimental testing ground to study biological plasticity.
Rulands and colleagues carried out a unique set of experiments in Panama where they removed the queen from paper wasp nests and then followed the reorganization process back to the intact society simultaneously on different scales of biological organization: from time-resolved profiling of brains using multi-omics of the brains to colony-level video recordings. Using theory, they showed that by balancing antagonistic molecular and colony-level processes these societies are able to distinguish between different kinds of perturbations affecting the nest: intrinsic perturbations, such as molecular noise, affect insects independently of each other and these perturbations are actively suppressed by the society. By contrast, extrinsic perturbations affect the entire society and the society reacts plasticly. Given the above, the authors conclude that by employing a self-organised multi-scale mechanism Polistes manages to overcome the seeming paradox between specialisation and plasticity.
S. Patalano et al., Cell Systems 13, 1–12 (2022)
Publication Highlights
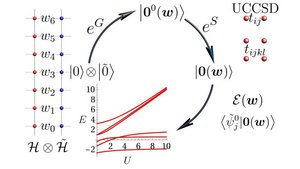
The full spectrum of a quantum many-body system in one shot
Quantum excited states underpin new states of matter, support biological processes such as vision, and determine opto-electronic properties of photovoltaic devices. Yet, while ground-state properties can be determined by rather accurate computational methods, there remains a need for theoretical and computational developments to target excited states efficiently. Inspired by the duplication of the Hilbert space used to study black-hole entanglement and the electronic pairing of conventional superconductivity, researchers from the Max Planck Institute for the Physics of Complex Systems and their collaborators from Munich and Modena have developed a new scheme to compute the full spectrum of a quantum many-body Hamiltonian, rather than only its ground or lowest-excited states. An important feature of their proposed scheme is that these spectra can be computed in a one-shot calculation. The scheme thus provides a novel variational platform to excited-state physics. It is also suitable for efficient implementation on quantum computers, so has the potential to enable unprecedented calculations of excited-state processes of quantum many-body systems.
C. L. Benavides-Riveros et al., Phys. Rev. Lett. 129, 066401 (2022), Editors' Suggestion
weiterlesenC. L. Benavides-Riveros et al., Phys. Rev. Lett. 129, 066401 (2022), Editors' Suggestion
Publication Highlights
Cells sense their way together
Much like animals can trace odors, cells also move toward certain chemicals. In fact, cells often do this in groups, which can be up to millions of individuals strong. But how do these cell populations manage to move together as a cohesive unit while following chemical cues? New work by Ricard Alert of the Max Planck Institute for the Physics of Complex Systems and collaborators shows that the answer lies in limitations in the ability of cells to sense chemicals at high concentrations. Thus, the work bridges scales by connecting the sensing of tiny molecules by individual cells to the shape and motion of an entire cell population, which can be centimeters or even larger in size. The work is important because it reveals a potentially general principle: Sensing—a distinguishing feature of living systems—governs the ability of cells to migrate in groups. This principle could operate in many other examples of collective migration, as cells and other living creatures can sense and follow a variety of stimuli, such as electric fields, temperature, and light intensity. Finally, the new results open a tantalizing question for future work: Has evolution pushed the sensing limitations of cells to ensure that they can follow chemical cues as a cohesive group? (Image credit: Mariona Esquerda Ciutat.)
R. Alert, A. Martínez-Calvo, and S. S. Datta, Phys. Rev. Lett. 128, 148101 (2022)
weiterlesenR. Alert, A. Martínez-Calvo, and S. S. Datta, Phys. Rev. Lett. 128, 148101 (2022)
Publication Highlights
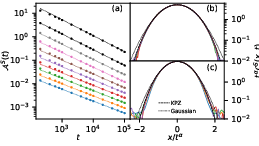
Anomalous dynamics and equilibration in the classical Heisenberg chain
The search for departures from standard hydrodynamics in many-body systems has yielded a number of promising leads, especially in low dimension. Researchers at the Max Planck Institute for the Physics of Complex Systems studied one of the simplest classical interacting lattice models, the nearest-neighbour Heisenberg chain, with temperature as tuning parameter.
Their numerics expose strikingly different spin dynamics between the antiferromagnet, where it is
largely diffusive, and the ferromagnet, where they observe strong evidence either of spin superdiffusion or an extremely slow crossover to diffusion. At low temperatures in the ferromagnet, they observe an extremely long-lived regime of
remarkably clean Kardar-Parisi-Zhang (KPZ) scaling (see figure). The anomalous behaviour also governs the equilibration after
a quench, and, remarkably, is apparent even at very high temperatures.
A. J. McRoberts, T. Bilitewski, M. Haque, and R. Moessner, Phys. Rev. B 105, L100403 (2022)
weiterlesenA. J. McRoberts, T. Bilitewski, M. Haque, and R. Moessner, Phys. Rev. B 105, L100403 (2022)
Publication Highlights
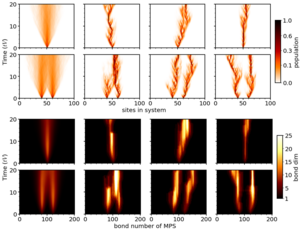
Non-Markovian Quantum State Diffusion: Matrix-product-state approach to the hierarchy of pure states
An important but challenging task is to treat mesoscopic systems that are coupled to a complex environment at finite temperature. Alexander Eisfeld of the Max Planck Institute for the Physics of Complex Systems and his collaborators have derived a stochastic hierarchy of matrix product states (HOMPS) for non-Markovian dynamics, which is numerically exact and efficient. In this way the exponential complexity of the problem can be reduced to scale polynomially with the number of particles and modes of the environment. An additional feature caused by the stochastic noise is that individual trajectories stay well localized. The validity and efficiency of HOMPS is demonstrated for the spin-boson model and long chains where each site is coupled to a structured, strongly non-Markovian environment.
X. Gao, J. Ren, A. Eisfeld, and Z. Shuai, Phys. Rev. A 105, L030202 (2022)
weiterlesenX. Gao, J. Ren, A. Eisfeld, and Z. Shuai, Phys. Rev. A 105, L030202 (2022)
Publication Highlights
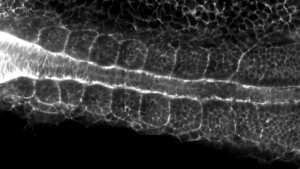
Left-right symmetry of zebrafish embryos requires surface tension
Bilateral symmetry of the vertebrate musculoskeletal system is necessary for proper function and its defects are associated with debilitating conditions, such as scoliosis. In a collaboration with biologists from the École polytechnique fédérale de Lausanne (EPFL) in Switzerland, Marko Popović of the Max Planck Institute for Physics of Complex Systems has studied the early stage of body segmentation using zebrafish as a model organism. They discovered that biochemical signalling and transcriptional processes that drive segmentation are not sufficient to explain the precision and symmetry of tissue shapes and sizes. However, they found that surface tension forces of the newly formed segments are a crucial component of the mechanism that is responsible for recovery and maintenance of the symmetric body plan. This discovery highlights the importance of physical interactions for precise and robust development of living beings.
S. R. Naganthan, M. Popovic, and A. C. Oates, Nature 605, 516-521 (2022)
weiterlesenS. R. Naganthan, M. Popovic, and A. C. Oates, Nature 605, 516-521 (2022)
Publication Highlights
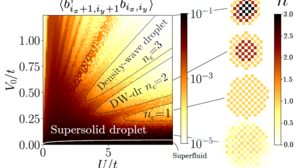
Novel quantum phases of droplets
Attractive forces are ubiquitous in nature: they glue very different objects ranging from atomic nuclei, droplets of water, to stars, galaxies, and black holes. Peter Karpov and Francesco Piazza of the Max Planck Institute for the Physics of Complex Systems have now demonstrated that highly tuneable attractive interactions can be engineered artificially using optical cavities, leading to various novel phases of quantum droplets of ultracold atoms. Upon tuning the cavity-mediated interactions it is possible to switch between superfluid droplets and incompressible water-like droplets, as well as to realise crystalline and even more exotic supersolid droplets combining superfluid and solid properties.
P. Karpov and F. Piazza, Phys. Rev. Lett. 128, 103201 (2022)
weiterlesenP. Karpov and F. Piazza, Phys. Rev. Lett. 128, 103201 (2022)