Quantum Aggregates

Quantum aggregates are assemblies of monomers (molecules, atoms, quantum dots...), where the monomers largely keep their individuality. However, interactions between the monomers can lead to collective phenomena, like superradiance or efficient excitation transfer. We study different kinds of aggregates (e.g. light harvesting systems, arrays of Rydberg atoms, self-assembled organic dyes...) Using various methods (ranging from Green-operator methods over stochastic Schroedinger equations to semicalssical surface hopping) we study optical and excitation transport in these systems. Of particular interest is the coupling of the excitation to nuclear degrees of freedom.

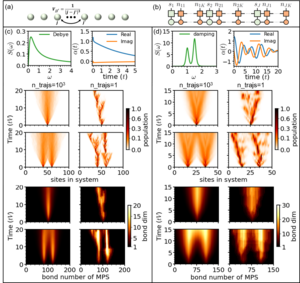
The hierarchy of pure states (HOPS) is a powerful stochastic wavefunction based approach to solve open quantum system problems with a non-Markovian environment.
Using a mapping of the hierachy of coupled stochasic differential equation to a Fock-space representation we can directly express the solution of HOPS in terms of matrix product states. This allows us now to handle much larger systems with more complex environments.

As example, on right the transfer dynamics of one or two excitations along a chain with around 100 molecules is shown. Two relevant cases are displayed (left: high temperature, right: low temperature and weakly damped vibrational modes. One nicely sees that the stochastics localizes individual trajectories, which in turn keeps the bond-dimensions of the matrix product states small.

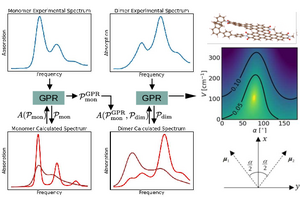
A common task  is the determination of system parameters from spectroscopy, where one compares the experimental spectrum with calculated spectra, that depend on the desired parameters.
Here we discuss an approach based on a machine learning technique, where the parameters for the numerical calculations are chosen from  Gaussian Process Regression (GPR).
This approach does not only quickly converge to an optimal parameter set, but in addition provides information about the complete parameter space, which allows for example to identify extended parameter regions where numerical spectra are consistent with the experimental one.  
We consider as example dimers of organic molecules and aim at extracting in particular the interaction between the monomers, and their mutual orientation.
We find that indeed the GPR gives reliable results which are in agreement with  direct calculations of these parameters using  quantum chemical methods.