Highlights
Publication Highlights
Interaction Dependent Heating and Atom Loss in a Periodically Driven Optical Lattice
Martin Reitter et al., Phys. Rev. Lett. 119, 200402
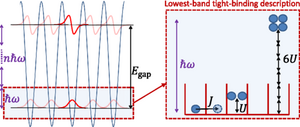
Time periodic driving, for example in the form of coherent radiation, is a standard tool for the manipulation of small quantum systems like single atoms. With the advent of highly controllable and well isolated quantum gases of neutral atoms, periodic driving has recently become a powerful tool also for the coherent control of many-body systems. A milestone is the possibility to couple the motion of neutral atoms to artificial magnetic fields, which allows to study quantum Hall physics with atomic quantum gases. However, periodically driven many-body systems suffer from unwanted intrinsic heating, the time scale of which should be large compared to the duration of the experiment. In a joint work of Scientists from Munich, Cambridge and Dresden, the interaction dependence of such intrinsic heating has now been measured for the first time and compared to theory. Interestingly, for sufficiently large driving frequencies, heating was found to be reduced via a new form of evaporative cooling.
Read moreTime periodic driving, for example in the form of coherent radiation, is a standard tool for the manipulation of small quantum systems like single atoms. With the advent of highly controllable and well isolated quantum gases of neutral atoms, periodic driving has recently become a powerful tool also for the coherent control of many-body systems. A milestone is the possibility to couple the motion of neutral atoms to artificial magnetic fields, which allows to study quantum Hall physics with atomic quantum gases. However, periodically driven many-body systems suffer from unwanted intrinsic heating, the time scale of which should be large compared to the duration of the experiment. In a joint work of Scientists from Munich, Cambridge and Dresden, the interaction dependence of such intrinsic heating has now been measured for the first time and compared to theory. Interestingly, for sufficiently large driving frequencies, heating was found to be reduced via a new form of evaporative cooling.
Publication Highlights
High-temperature nonequilibrium Bose condensation induced by a hot needle
Alexander Schnell et al., Phys. Rev. Lett. 119, 140602
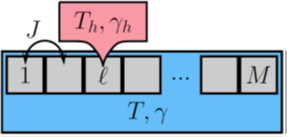
When a physical system is brought in weak thermal contact with an environment of temperature T, it will appproach an equilibrium state. The properties of this state depend on the temperature of the environment only. For example, a quantum gas of bosonic particles will form a Bose-Einstein condensate, where a macroscopic fraction the particles occupies the same state, below a condensation temperature T_c. In contrast, when a system is coupled to two heat baths of different temperatures T_1 and T_2, the situation changes in a fundamental way. In this case the system will assume a non-equilibrium steady state, which depends on the very details of both baths and not simply on their temperatures. It is an interesting question in how far this fact can be used to manipulate the far-from equilibrium state of the system in a controlled fashion by bath engineering. In this paper, we describe an astonishing effect: a Bose gas that is embedded in an environment of temperature T>>T_c can form a Bose condensate when coupled to a "hot needle", a second local bath of even larger temperature T_h>>T. Moreover, depending on the parameters and unlike in thermal equilibrium, the condensate can also be formed in an excited state of the system.
Read moreWhen a physical system is brought in weak thermal contact with an environment of temperature T, it will appproach an equilibrium state. The properties of this state depend on the temperature of the environment only. For example, a quantum gas of bosonic particles will form a Bose-Einstein condensate, where a macroscopic fraction the particles occupies the same state, below a condensation temperature T_c. In contrast, when a system is coupled to two heat baths of different temperatures T_1 and T_2, the situation changes in a fundamental way. In this case the system will assume a non-equilibrium steady state, which depends on the very details of both baths and not simply on their temperatures. It is an interesting question in how far this fact can be used to manipulate the far-from equilibrium state of the system in a controlled fashion by bath engineering. In this paper, we describe an astonishing effect: a Bose gas that is embedded in an environment of temperature T>>T_c can form a Bose condensate when coupled to a "hot needle", a second local bath of even larger temperature T_h>>T. Moreover, depending on the parameters and unlike in thermal equilibrium, the condensate can also be formed in an excited state of the system.
Publication Highlights
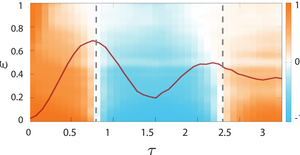
Observation of a dynamical quantum phase transition
Petar Jurcevic et al., PRL 119, 080501
Today, the equilibrium properties of quantum matter are theoretically described with great success. Yet, in recent years pioneering experiments have created quantum states beyond this equilibrium paradigm. Understanding properties of such nonequilibrium quantum states on a general level provides a significant challenge. Jurcevic at el. have now experimentally observed for the first time a phenomenon - a dynamical quantum phase transition - which promises to provide a general framework to identify and predict such general principles of quantum dynamics.
See also the Physics Viewpoint: Quantum Phase Transitions Go Dynamical
Read moreToday, the equilibrium properties of quantum matter are theoretically described with great success. Yet, in recent years pioneering experiments have created quantum states beyond this equilibrium paradigm. Understanding properties of such nonequilibrium quantum states on a general level provides a significant challenge. Jurcevic at el. have now experimentally observed for the first time a phenomenon - a dynamical quantum phase transition - which promises to provide a general framework to identify and predict such general principles of quantum dynamics.
See also the Physics Viewpoint: Quantum Phase Transitions Go Dynamical
Publication Highlights
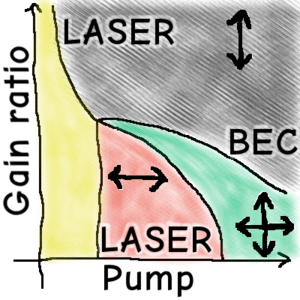
Pump-Power-Driven Mode Switching in a Microcavity Device and Its Relation to Bose-Einstein Condensation
H.A.M. Leymann et al., Phys. Rev. X 7, 021045 (2017)
We investigate the switching of the coherent emission mode of a bimodal microcavity device, occurring when the pump power is varied. We compare experimental data to theoretical results and identify the underlying mechanism based on the competition between the effective gain, on the one hand, and the intermode kinetics, on the other. When the pumping is ramped up, above a threshold, the mode with the largest effective gain starts to emit coherent light, corresponding to lasing. In contrast, in the limit of strong pumping, it is the intermode kinetics that determines which mode acquires a large occupation and shows coherent emission. We point out that this latter mechanism is akin to the equilibrium Bose-Einstein condensation of massive bosons. Thus, the mode switching in our microcavity device can be viewed as a minimal instance of Bose-Einstein condensation of photons. Moreover, we show that the switching from one cavity mode to the other always occurs via an intermediate phase where both modes are emitting coherent light and that it is associated with both superthermal intensity fluctuations and strong anticorrelations between both modes.
Read moreWe investigate the switching of the coherent emission mode of a bimodal microcavity device, occurring when the pump power is varied. We compare experimental data to theoretical results and identify the underlying mechanism based on the competition between the effective gain, on the one hand, and the intermode kinetics, on the other. When the pumping is ramped up, above a threshold, the mode with the largest effective gain starts to emit coherent light, corresponding to lasing. In contrast, in the limit of strong pumping, it is the intermode kinetics that determines which mode acquires a large occupation and shows coherent emission. We point out that this latter mechanism is akin to the equilibrium Bose-Einstein condensation of massive bosons. Thus, the mode switching in our microcavity device can be viewed as a minimal instance of Bose-Einstein condensation of photons. Moreover, we show that the switching from one cavity mode to the other always occurs via an intermediate phase where both modes are emitting coherent light and that it is associated with both superthermal intensity fluctuations and strong anticorrelations between both modes.
Publication Highlights
Neutron scattering in the proximate quantum spin liquid a-RuCl3
Arnab Banerjee et al. Science 356, 1055 (2017)
The Kitaev quantum spin liquid (KQSL) is an exotic emergent state of matter exhibiting Majorana fermion and gauge flux excitations. The magnetic insulator ?-RuCl3 is thought to realize a proximate KQSL. We used neutron scattering on single crystals of ?-RuCl3 to reconstruct dynamical correlations in energy-momentum space. We discovered highly unusual signals, including a column of scattering over a large energy interval around the Brillouin zone center, which is very stable with temperature. This finding is consistent with scattering from the Majorana excitations of a KQSL. Other, more delicate experimental features can be transparently associated with perturbations to an ideal model. Our results encourage further study of this prototypical material and may open a window into investigating emergent magnetic Majorana fermions in correlated materials.
See also: A. Banerjee et al. Nature Materials, 15, 733 (2016).
Read moreThe Kitaev quantum spin liquid (KQSL) is an exotic emergent state of matter exhibiting Majorana fermion and gauge flux excitations. The magnetic insulator ?-RuCl3 is thought to realize a proximate KQSL. We used neutron scattering on single crystals of ?-RuCl3 to reconstruct dynamical correlations in energy-momentum space. We discovered highly unusual signals, including a column of scattering over a large energy interval around the Brillouin zone center, which is very stable with temperature. This finding is consistent with scattering from the Majorana excitations of a KQSL. Other, more delicate experimental features can be transparently associated with perturbations to an ideal model. Our results encourage further study of this prototypical material and may open a window into investigating emergent magnetic Majorana fermions in correlated materials.
See also: A. Banerjee et al. Nature Materials, 15, 733 (2016).
Publication Highlights
Equilibration and Order in Quantum Floquet Matter
R. Moessner and S. L. Sondhi, Nature Physics 13, 424 (2017)
Equilibrium thermodynamics is characterized by two fundamental ideas: thermalization—that systems approach a late time thermal state; and phase structure—that thermal states exhibit singular changes as various parameters characterizing the system are changed. We summarize recent progress that has established generalizations of these ideas to periodically driven, or Floquet, closed quantum systems. This has resulted in the discovery of entirely new phases which exist only out of equilibrium, such as the ?-spin glass/Floquet time crystal.
This is a progress article. For related original work see: Phase Structure of Driven Quantum Systems, Khemani et al. Phys. Rev. Lett. 116, 250401 (2016).
Read moreEquilibrium thermodynamics is characterized by two fundamental ideas: thermalization—that systems approach a late time thermal state; and phase structure—that thermal states exhibit singular changes as various parameters characterizing the system are changed. We summarize recent progress that has established generalizations of these ideas to periodically driven, or Floquet, closed quantum systems. This has resulted in the discovery of entirely new phases which exist only out of equilibrium, such as the ?-spin glass/Floquet time crystal.
This is a progress article. For related original work see: Phase Structure of Driven Quantum Systems, Khemani et al. Phys. Rev. Lett. 116, 250401 (2016).
Publication Highlights
Competition between histone and transcription factor binding regulates the onset of transcription in zebrafish embryos
Shai R Joseph et al. eLife 2017;6:e23326
Upon fertilization, the genome of animal embryos remains transcriptionally inactive until the maternal-to-zygotic transition. At this time, the embryo takes control of its development and transcription begins. How the onset of zygotic transcription is regulated remains unclear. Here, we show that a dynamic competition for DNA binding between nucleosome-forming histones and transcription factors regulates zebrafish genome activation. Taking a quantitative approach, we found that the concentration of non-DNA-bound core histones sets the time for the onset of transcription. The reduction in nuclear histone concentration that coincides with genome activation does not affect nucleosome density on DNA, but allows transcription factors to compete successfully for DNA binding. In agreement with this, transcription factor binding is sensitive to histone levels and the concentration of transcription factors also affects the time of transcription. Our results demonstrate that the relative levels of histones and transcription factors regulate the onset of transcription in the embryo.
Read moreUpon fertilization, the genome of animal embryos remains transcriptionally inactive until the maternal-to-zygotic transition. At this time, the embryo takes control of its development and transcription begins. How the onset of zygotic transcription is regulated remains unclear. Here, we show that a dynamic competition for DNA binding between nucleosome-forming histones and transcription factors regulates zebrafish genome activation. Taking a quantitative approach, we found that the concentration of non-DNA-bound core histones sets the time for the onset of transcription. The reduction in nuclear histone concentration that coincides with genome activation does not affect nucleosome density on DNA, but allows transcription factors to compete successfully for DNA binding. In agreement with this, transcription factor binding is sensitive to histone levels and the concentration of transcription factors also affects the time of transcription. Our results demonstrate that the relative levels of histones and transcription factors regulate the onset of transcription in the embryo.
Publication Highlights
Colloquium: Atomic quantum gases in periodically driven optical lattices
André Eckardt, Rev. Mod. Phys. 89, 011004 (2017)
Time-periodic forcing in the form of coherent radiation is a standard tool for the coherent manipulation of small quantum systems like single atoms. In the last years, periodic driving has more and more also been considered as a means for the coherent control of many-body systems. In particular, experiments with ultracold quantum gases in optical lattices subjected to periodic driving in the lower kilohertz regime have attracted much attention. Milestones include the observation of dynamic localization, the dynamic control of the quantum phase transition between a bosonic superfluid and a Mott insulator, as well as the dynamic creation of strong artificial magnetic fields and topological band structures. This Colloquium reviews these recent experiments and their theoretical description. Moreover, fundamental properties of periodically driven many-body systems are discussed within the framework of Floquet theory, including heating, relaxation dynamics, anomalous topological edge states, and the response to slow parameter variations.
Read moreTime-periodic forcing in the form of coherent radiation is a standard tool for the coherent manipulation of small quantum systems like single atoms. In the last years, periodic driving has more and more also been considered as a means for the coherent control of many-body systems. In particular, experiments with ultracold quantum gases in optical lattices subjected to periodic driving in the lower kilohertz regime have attracted much attention. Milestones include the observation of dynamic localization, the dynamic control of the quantum phase transition between a bosonic superfluid and a Mott insulator, as well as the dynamic creation of strong artificial magnetic fields and topological band structures. This Colloquium reviews these recent experiments and their theoretical description. Moreover, fundamental properties of periodically driven many-body systems are discussed within the framework of Floquet theory, including heating, relaxation dynamics, anomalous topological edge states, and the response to slow parameter variations.
Publication Highlights
Growth and Division of Active Droplets Provides a Model for Protocells
D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Jülicher, Nature Physics (2016)
We show that liquid droplets that are driven away from thermodynamic equilibrium by chemical reactions can undergo cycles of growth and division reminiscent of living cells. We propose such active droplets as simple models for prebiotic protocells. Our work shows that protocells could have been able to propagate and divide without having established membranes.
See also coverage in Chemistry World and two articles in Quanta Magazine: article 1 and article 2.
Read moreWe show that liquid droplets that are driven away from thermodynamic equilibrium by chemical reactions can undergo cycles of growth and division reminiscent of living cells. We propose such active droplets as simple models for prebiotic protocells. Our work shows that protocells could have been able to propagate and divide without having established membranes.
See also coverage in Chemistry World and two articles in Quanta Magazine: article 1 and article 2.
Publication Highlights
U(1) Wilson lattice gauge theories in digital quantum simulators
Christine Muschik, Markus Heyl, et al., arXiv:1612.08653
Lattice gauge theories describe fundamental phenomena in nature, but calculating their real-time dynamics on classical computers appears to be notoriously difficult. Digital quantum simulation has been proposed as a general strategy to solve such computationally hard problems on a programmable quantum device instead of using conventional computers. Recently, an experiment has demonstrated for the first time a digital quantum simulation of a lattice gauge theory on a small-scale quantum computer made of trapped ions. This work has been selected by the magazine Physics World as one of the top ten breakthroughs in physics in 2016. Now, a detailed theoretical analysis of the experimentally used scheme has been published which studies in detail the scheme's performance, robustness against various error sources, and scalability.
See also coverage in Physics World and the experimental work .
Read moreLattice gauge theories describe fundamental phenomena in nature, but calculating their real-time dynamics on classical computers appears to be notoriously difficult. Digital quantum simulation has been proposed as a general strategy to solve such computationally hard problems on a programmable quantum device instead of using conventional computers. Recently, an experiment has demonstrated for the first time a digital quantum simulation of a lattice gauge theory on a small-scale quantum computer made of trapped ions. This work has been selected by the magazine Physics World as one of the top ten breakthroughs in physics in 2016. Now, a detailed theoretical analysis of the experimentally used scheme has been published which studies in detail the scheme's performance, robustness against various error sources, and scalability.
See also coverage in Physics World and the experimental work .