|
We analyze possible controlling at ultralow temperatures
the atom-atom interaction by a nonresonant optocal laser.
Including into consideration the finiteness of the laser wavelength 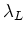 or the alteration of the laser polarization makes the problem of ultracold atom-atom collisions
in the laser field nonseparable over both angular variables or the alteration of the laser polarization makes the problem of ultracold atom-atom collisions
in the laser field nonseparable over both angular variables
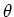 and and 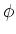 (scattering angles). It leads to essentially anisotropic scattering. For treating this problem we developed an approach without usual partial-wave expansion [1]. Here the angular part of the scattering wave-function is approximated in the spirit of the discrete-variable representation [2] or Lagrange-mesh [3]. The method was suggested in [4] for solving nonseparable two-dimensional scattering problem and extended to three-dimensional atoms in strong fields [5,6]. (scattering angles). It leads to essentially anisotropic scattering. For treating this problem we developed an approach without usual partial-wave expansion [1]. Here the angular part of the scattering wave-function is approximated in the spirit of the discrete-variable representation [2] or Lagrange-mesh [3]. The method was suggested in [4] for solving nonseparable two-dimensional scattering problem and extended to three-dimensional atoms in strong fields [5,6].
With this approach we find considerable influence of a nonresonant optical laser of intensity
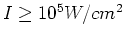 on the Cs-Cs ultracold collisions: on the Cs-Cs ultracold collisions:
1) In such field the scattering becomes strongly anisotropic even in the region of ulralow colliding energies where the 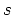 -wave dominates at -wave dominates at  . I.e. the usual scattering length approach . I.e. the usual scattering length approach
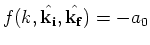 does not work and one has to analyze the stability of BEC for unusual behavior of the amplitude does not work and one has to analyze the stability of BEC for unusual behavior of the amplitude
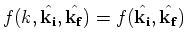 at at
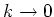 . At that the amplitude may be strongly dependent on the . At that the amplitude may be strongly dependent on the 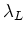 , on the relative atom-atom orientation with respect to the field , on the relative atom-atom orientation with respect to the field
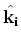 and on the scattering angle and on the scattering angle
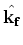 , even changes the sign at some , even changes the sign at some
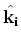 and and
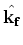 . .
2) The maximum anisotropy is developed for the linear laser polarization. The differential cross section may change from zero at some angles up to hundreds a.u. in the direction of polarization.
3) Strong dependence on the laser wavelength 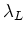 is shown at the optical region as is shown at the optical region as 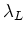 becomes shorter than the critical value becomes shorter than the critical value
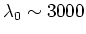 nm (of the de Broglie wave nm (of the de Broglie wave 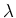 ) defining the region ) defining the region
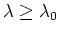 of the of the 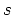 -wave domination at -wave domination at 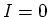 . .
It would be interesting to include the considered effects of anysotropy in ulralow collisions into the theoretical models for BEC and to test experimentally.
[1] V.S. Melezhik and Chi-Yu Hu, Phys. Rev. Lett. 90, 083202 (2003
[2] J.V. Lill, G.A. Parker, and J.C. Light, Chem. Phys. Lett. 89, 483 (1982); J.C. Light and T. Carrington, Jr., Adv. Chem. Phys. 114, 263
(2000)
[3] D. Baye and P.-H. Heenen, J. Phys. A19, 2041 (1986)
[4] V.S. Melezhik, J. Comput. Phys. 92, 67 (1991)
[5] V.S. Melezhik, Phys. Rev. A48, 4528 (1993)
[6] P. Fassbinder and W. Schweizer, Phys. Rev. A53, 2135 (1996)
|