Highlights
Publication Highlights
Activity-enhanced elasticity in entangled polymer solutions
One of the key achievements of equilibrium polymer physics is the prediction of scaling laws governing the viscoelastic properties of entangled polymer systems, validated in both natural polymers, such as DNA, and synthetic polymers, including polyethylene, which form materials like plastics. Recently, focus has shifted to active polymer systems composed of motile units driven far from equilibrium, such as California blackworms, self-propelled biopolymers, and soft robotic grippers. Despite their growing importance, their viscoelastic properties and universal scaling laws are not yet understood.
Christina Kurzthaler of the Max Planck Institute for the Physics of Complex Systems and her collaborators at the Technische Universität Darmstadt and the Heinrich Heine-Universität Düsseldorf have now investigated the viscoelastic properties of highly-entangled, flexible self-propelled polymers using Brownian dynamics simulations and scaling arguments. Their results demonstrate that activity enhances the elasticity by orders of magnitude due to the emergence of grip forces at entanglement points. Furthermore, activity fluidises the suspension, which is manifested by a lower viscosity than in the passive counterpart. These insights may open new avenues for designing activity-responsive polymeric materials.
Davide Breoni, Christina Kurzthaler, Benno Liebchen, Harmut Löwen, and Suvendu Mandal, Nat. Commun. 16, 5305 (2025)
See also the press release by the Heinrich-Heine Universität Düsseldorf (in German).
weiterlesenChristina Kurzthaler of the Max Planck Institute for the Physics of Complex Systems and her collaborators at the Technische Universität Darmstadt and the Heinrich Heine-Universität Düsseldorf have now investigated the viscoelastic properties of highly-entangled, flexible self-propelled polymers using Brownian dynamics simulations and scaling arguments. Their results demonstrate that activity enhances the elasticity by orders of magnitude due to the emergence of grip forces at entanglement points. Furthermore, activity fluidises the suspension, which is manifested by a lower viscosity than in the passive counterpart. These insights may open new avenues for designing activity-responsive polymeric materials.
Davide Breoni, Christina Kurzthaler, Benno Liebchen, Harmut Löwen, and Suvendu Mandal, Nat. Commun. 16, 5305 (2025)
See also the press release by the Heinrich-Heine Universität Düsseldorf (in German).
Publication Highlights
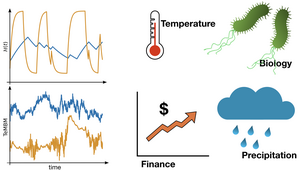
New random walk model elucidates hidden spatiotemporal patterns in complex systems
Recent experiments tracking organelles in biological cells or financial-market data report clear variations in their spatiotemporal scaling properties. Samudrajit Thapa and Holger Kantz of the Max Planck Institute for the Physics of Complex Systems, together with collaborators, have now introduced a new random-walk model, Telegraphic Multifractional Brownian Motion (TeMBM), to unravel the physical mechanisms underlying
the scaling properties in such systems. Thee researchers provide a method to identify TeMBM in experimental data, which they apply to time series from climate, biology, and finance. TeMBM builds on long-range correlated stochastic models originally developed by Kolmogorov, Mandelbrot, and van Ness, the so-called fractional Brownian motion (FBM). FBM exhibits statistically-similar patterns at all time scales and
is characterised by a constant Hurst exponent. FBM finds applications in finance or biology due to their distinct correlations.
However, FBM cannot explain the highly complicated scaling phenomena observed in many complex systems in which the estimated values of the Hurst exponent are seen to vary over time. TeMBM is a generalisation of FBM designed to incorporate this property. The authors show that TeMBM can mimic properties such as the probability distribution of the Hurst exponents reported in single-particle tracking experiments. They also provide a simple yet efficient method to distinguish between TeMBM and conventional FBM in experimental data. The framework of TeMBM promises the detection and description of unexpected commonalities in various systems unrelated at first glance.
Michał Balcerek, Samudrajit Thapa, Krzysztof Burnecki, Holger Kantz, Ralf Metzler, Agnieszka Wyłomańska, and Aleksei Chechkin, Phys. Rev. Lett. 134, 197101 (2025)
weiterlesenHowever, FBM cannot explain the highly complicated scaling phenomena observed in many complex systems in which the estimated values of the Hurst exponent are seen to vary over time. TeMBM is a generalisation of FBM designed to incorporate this property. The authors show that TeMBM can mimic properties such as the probability distribution of the Hurst exponents reported in single-particle tracking experiments. They also provide a simple yet efficient method to distinguish between TeMBM and conventional FBM in experimental data. The framework of TeMBM promises the detection and description of unexpected commonalities in various systems unrelated at first glance.
Michał Balcerek, Samudrajit Thapa, Krzysztof Burnecki, Holger Kantz, Ralf Metzler, Agnieszka Wyłomańska, and Aleksei Chechkin, Phys. Rev. Lett. 134, 197101 (2025)
Publication Highlights
Impossible ecologies
What are the general principles that determine whether species can coexist stably in an ecological community? This has been a central problem in theoretical ecology and in complex systems theory ever since, half a century ago, mathematical ideas from random matrix theory began to allow identification of these principles for large numbers of species.
Now, Yu Meng, Szabolcs Horvát, Carl Modes, and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems, the Max Planck Institute of Molecular Cell Biology and Genetics, and the Center for Systems Biology Dresden have found a new approach to address these questions, based on exhaustive analysis of all networks of competitive, mutualistic, and predator-prey interactions of small numbers of species. By analysing hundreds of thousands of networks numerically and establishing a mathematical theorem relating the possibility of stability of coexistence in a community to its subcommunities, the authors discovered how the possibility of stable coexistence is hugely affected by details of the network of ecological interactions that cannot be captured by approaches based on random matrix theory. They also revealed curious "impossible ecologies" in which stable coexistence is nontrivially impossible. This work thus shows how details of ecological interactions can swamp or overcome general principles of ecological stability.
The authors are now collaborating with the recently arrived research groups in mathematics at the Center for Systems Biology Dresden to extend their numerical approaches and exact results to larger ecological communities using new mathematical tools.
Yu Meng, Szabolcs Horvát, Carl D. Modes, and Pierre A. Haas, Cell Syst. 16, in press (2025)
weiterlesenNow, Yu Meng, Szabolcs Horvát, Carl Modes, and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems, the Max Planck Institute of Molecular Cell Biology and Genetics, and the Center for Systems Biology Dresden have found a new approach to address these questions, based on exhaustive analysis of all networks of competitive, mutualistic, and predator-prey interactions of small numbers of species. By analysing hundreds of thousands of networks numerically and establishing a mathematical theorem relating the possibility of stability of coexistence in a community to its subcommunities, the authors discovered how the possibility of stable coexistence is hugely affected by details of the network of ecological interactions that cannot be captured by approaches based on random matrix theory. They also revealed curious "impossible ecologies" in which stable coexistence is nontrivially impossible. This work thus shows how details of ecological interactions can swamp or overcome general principles of ecological stability.
The authors are now collaborating with the recently arrived research groups in mathematics at the Center for Systems Biology Dresden to extend their numerical approaches and exact results to larger ecological communities using new mathematical tools.
Yu Meng, Szabolcs Horvát, Carl D. Modes, and Pierre A. Haas, Cell Syst. 16, in press (2025)
Publication Highlights
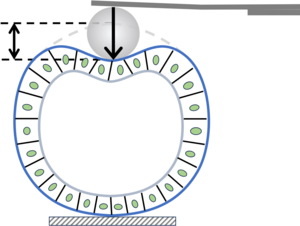
Mechanics of poking a cyst
Just as poking a tomato in a supermarket reveals the immediacy of its comestibility, poking a cyst of cells can reveal the mechanical state of the cells forming the cyst. Such indentation tests are widely used biophysical tools, but they require a mechanical model for the relation between the force and the indentation of the sample. For these biological samples, predictions of this force-indentation relation for simple materials cannot however be expected to hold.
Shiheng Zhao and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute of Molecular Cell Biology and Genetics have now shown that biomechanical properties such as nonlinear elasticity and prestress arising from the cortical mechanics and contracility of cells can even give rise to new scaling exponents in this force-displacement relation. The authors used numerical simulations to show that their exact predictions are robust, even for thick bological samples such as cysts of cells, and found their predicted exponents in existing experimental data of cyst indentation. Their work thus provides the theoretical basis for experimental understanding of how different cell biological processes conspire to control the mechanics of cysts.
Shiheng Zhao and Pierre A. Haas, Phys. Rev. Lett. 134, 228402 (2025), highlighted as an Editors' Suggestion
weiterlesenShiheng Zhao and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute of Molecular Cell Biology and Genetics have now shown that biomechanical properties such as nonlinear elasticity and prestress arising from the cortical mechanics and contracility of cells can even give rise to new scaling exponents in this force-displacement relation. The authors used numerical simulations to show that their exact predictions are robust, even for thick bological samples such as cysts of cells, and found their predicted exponents in existing experimental data of cyst indentation. Their work thus provides the theoretical basis for experimental understanding of how different cell biological processes conspire to control the mechanics of cysts.
Shiheng Zhao and Pierre A. Haas, Phys. Rev. Lett. 134, 228402 (2025), highlighted as an Editors' Suggestion
Publication Highlights
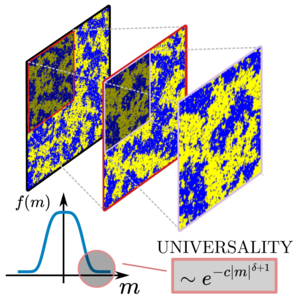
Where does Universality hide?
The central limit theorem is one of the most important achievements in statistics and probability theory. It ensures that for many systems found in nature, the features observed (be they heights, dice rolls, or test scores) are always "normal", meaning that they follow a Gaussian distribution. However, when all the elements of the system interact and influence each other, this fundamental theorem can be broken and lead to uncontrolled dramatic behaviours. Explaining these remained a key open problem in statistical mechanics.
Now, Gianluca Teza of the Max Planck Institute for the Physics of Complex Systems and Attilio Stella of the University of Padova have built a unifying picture to close this gap. They have shown how the breakdown of the central limit theorem leads to specific universal and non-universal features that they found to be determined solely by extremely rare events that would never be observed in non-interacting systems. The validity of these findings was proved with exact analytical calculations in two paradigmatic models. Their results thus confirm and extend long-standing conjectures in statistical mechanics, while opening a series of applications ranging from computational physics to condensed matter.
Gianluca Teza and Attilio L. Stella, Phys. Rev. Lett. 134, 127102 (2025)
weiterlesenNow, Gianluca Teza of the Max Planck Institute for the Physics of Complex Systems and Attilio Stella of the University of Padova have built a unifying picture to close this gap. They have shown how the breakdown of the central limit theorem leads to specific universal and non-universal features that they found to be determined solely by extremely rare events that would never be observed in non-interacting systems. The validity of these findings was proved with exact analytical calculations in two paradigmatic models. Their results thus confirm and extend long-standing conjectures in statistical mechanics, while opening a series of applications ranging from computational physics to condensed matter.
Gianluca Teza and Attilio L. Stella, Phys. Rev. Lett. 134, 127102 (2025)
Publication Highlights
Giant molecules assembled atom-by-atom
Optical tweezers allow researchers to trap and manipulate atoms in laser beams, a technology at the core of quantum simulation and computing using ultracold atoms. Individual tweezers cannot be brought closer together than a few hundred nanometres. This distance is thousands of times bigger than a typical chemical bond, dooming the atoms to a lonely existence. However, when one of the atoms is promoted to a highly excited Rydberg state, its valence electron orbits far from the nucleus, even passing by a second atom held in a distant tweezer. This could allow exotic long-range molecules to form, bound by the attractive interatomic interaction mediated by the scattering of the electron off of the ground-state atom.
Now, Aileen Durst and Matthew Eiles of the Max Planck Institute for the Physics of Complex Systems and their collaborators at Durham University have made this idea a reality. The experimentalists at Durham University begin with isolated rubidium and caesium atoms in separate traps. After exciting the rubidium atom to a Rydberg state, they image the atoms to observe the molecular formation. By selecting spatially anisotropic Rydberg states and varying the tweezer separation, they confirm the theoretical predictions for the vibrational energies, alignment, and chemical bond length of the molecule made by the researchers at the Max Planck Institute for the Physics of Complex Systems. In the future, these capabilities may be applied to quantum simulators and computers that harness atoms excited to Rydberg states, and can be used to assemble molecules “on demand" from their individual components.
Alexander Guttridge, Tom R. Hepworth, Daniel K. Ruttley, Aileen A. T. Durst, Matthew T. Eiles, and Simon L. Cornish, Phys. Rev. Lett. 134, 133401 (2025)
weiterlesenNow, Aileen Durst and Matthew Eiles of the Max Planck Institute for the Physics of Complex Systems and their collaborators at Durham University have made this idea a reality. The experimentalists at Durham University begin with isolated rubidium and caesium atoms in separate traps. After exciting the rubidium atom to a Rydberg state, they image the atoms to observe the molecular formation. By selecting spatially anisotropic Rydberg states and varying the tweezer separation, they confirm the theoretical predictions for the vibrational energies, alignment, and chemical bond length of the molecule made by the researchers at the Max Planck Institute for the Physics of Complex Systems. In the future, these capabilities may be applied to quantum simulators and computers that harness atoms excited to Rydberg states, and can be used to assemble molecules “on demand" from their individual components.
Alexander Guttridge, Tom R. Hepworth, Daniel K. Ruttley, Aileen A. T. Durst, Matthew T. Eiles, and Simon L. Cornish, Phys. Rev. Lett. 134, 133401 (2025)
Publication Highlights
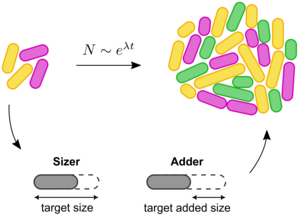
From noisy cell size control to population growth
Single-cell experiments have revealed substantial variability in generation times, growth rates, but also in birth and division sizes between genetically identical cells. Understanding how these fluctuations determine the fitness of the population, i.e., its long-term growth rate, is necessary in any quantitative theory of evolution.
Now, Arthur Genthon of the Max Planck Institute for the Physics of Complex Systems has developed a biologically relevant model which accounts for the stochasticity in single-cell growth rates, birth sizes, and division sizes. This model allows for expressions for the population growth rate and mean birth size in the population to be derived in terms of single-cell fluctuations. Allowing division sizes to fluctuate reveals how the mechanism of cell size control ("timer", "sizer", or "adder") influences population growth. Arthur Genthon finds that, surprisingly, fluctuations in single-cell growth rates can be beneficial for population growth when slow-growing cells tend to divide at smaller sizes than fast-growing cells.
Arthur Genthon, Phys. Rev. E 111, 034407 (2025), highlighted as an Editors' Suggestion
weiterlesenNow, Arthur Genthon of the Max Planck Institute for the Physics of Complex Systems has developed a biologically relevant model which accounts for the stochasticity in single-cell growth rates, birth sizes, and division sizes. This model allows for expressions for the population growth rate and mean birth size in the population to be derived in terms of single-cell fluctuations. Allowing division sizes to fluctuate reveals how the mechanism of cell size control ("timer", "sizer", or "adder") influences population growth. Arthur Genthon finds that, surprisingly, fluctuations in single-cell growth rates can be beneficial for population growth when slow-growing cells tend to divide at smaller sizes than fast-growing cells.
Arthur Genthon, Phys. Rev. E 111, 034407 (2025), highlighted as an Editors' Suggestion
Publication Highlights
Fragmented superconductivity in the Hubbard model as solitons in Ginzburg–Landau theory
High-temperature superconductivity, the phenomenon allowing current to flow without resistance in materials near room temperature, is one of the most captivating problems of modern condensed matter physics due to its potentially groundbreaking technological implications. Nevertheless, both its experimental realization and theoretical description have proven to be extraordinarily challenging. Recent experimental and numerical studies have revealed that the interplay between strong electron interactions and geometric frustration can induce superconductivity in 2D models, typically intertwined with a wave pattern in the electronic density.
Now Hannes Karlsson and Alex Wietek of the Max Planck Institute of the Physics of Complex Systems, together with collaborators at the Barcelona Institute of Science and Technology and at the Flatiron Institute, have delved into the properties of this intertwined state, demonstrating by large-scale numerical simulations that in the presence of charge density modulations, superconductivity is characterized by the condensation of electron pairs into a superposition of several macroscopic wavefunctions. This leads to the formation of a "fragmented" condensate, both in the presence and absence of a background magnetic flux. The researchers have also illustrated how a simple analytical model, requiring remarkably few experimentally measurable parameters, can accurately describe the behavior of the superconducting wavefunctions obtained in their numerical experiments. Their approach thus provides a readily applicable tool for fitting experimental results to analytical predictions in the quest for superconductivity in strongly-correlated materials.
Niccolò Baldelli, Hannes Karlsson, Benedikt Kloss, Matthew Fishman, and Alexander Wietek, npj Quantum Materials 10, 22 (2025)
weiterlesenNow Hannes Karlsson and Alex Wietek of the Max Planck Institute of the Physics of Complex Systems, together with collaborators at the Barcelona Institute of Science and Technology and at the Flatiron Institute, have delved into the properties of this intertwined state, demonstrating by large-scale numerical simulations that in the presence of charge density modulations, superconductivity is characterized by the condensation of electron pairs into a superposition of several macroscopic wavefunctions. This leads to the formation of a "fragmented" condensate, both in the presence and absence of a background magnetic flux. The researchers have also illustrated how a simple analytical model, requiring remarkably few experimentally measurable parameters, can accurately describe the behavior of the superconducting wavefunctions obtained in their numerical experiments. Their approach thus provides a readily applicable tool for fitting experimental results to analytical predictions in the quest for superconductivity in strongly-correlated materials.
Niccolò Baldelli, Hannes Karlsson, Benedikt Kloss, Matthew Fishman, and Alexander Wietek, npj Quantum Materials 10, 22 (2025)
Publication Highlights
Unbuckling mechanics of epithelial monolayers under compression
Many of the wrinkly shapes that appear throughout development, including the gyrations of the brain and the villi of the gut, arise from mechanical instabilities. These mechanical instabilities of tissues consisting of individual cells can be very different, however, from classical instabilities such as the buckling of a sheet of paper under compression.
Now Chandraniva Guha Ray and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute of Molecular Cell Biology and Genetics have discovered curious "unbuckling" behaviour in a minimal mechanical model of an epithelial monolayer under compression. Unlike a sheet of paper, the buckling amplitude of which increases with increasing compression, and at sufficiently large compression, the buckling amplitude of this cell sheet can decrease with increasing compression. The authors explained how this unbuckling is associated with a bifurcation that occurs when all cells constrict to triangular shapes. Their calculation reveals how this results in a huge stiffening of the cell sheet to further compression. This provides a mechanism for the absorption of compressive stresses by tissue folds such as the cephalic furrow in the fruit fly Drosophila.
Chandraniva Guha Ray and Pierre A. Haas, Phys. Rev. Lett. 134, 118402 (2025), highlighted as an Editors' Suggestion
weiterlesenNow Chandraniva Guha Ray and Pierre Haas of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute of Molecular Cell Biology and Genetics have discovered curious "unbuckling" behaviour in a minimal mechanical model of an epithelial monolayer under compression. Unlike a sheet of paper, the buckling amplitude of which increases with increasing compression, and at sufficiently large compression, the buckling amplitude of this cell sheet can decrease with increasing compression. The authors explained how this unbuckling is associated with a bifurcation that occurs when all cells constrict to triangular shapes. Their calculation reveals how this results in a huge stiffening of the cell sheet to further compression. This provides a mechanism for the absorption of compressive stresses by tissue folds such as the cephalic furrow in the fruit fly Drosophila.
Chandraniva Guha Ray and Pierre A. Haas, Phys. Rev. Lett. 134, 118402 (2025), highlighted as an Editors' Suggestion
Publication Highlights
Altermagnetism recognised among "Top 10 Breakthroughs of 2024"
The discovery of altermagnetism has been included by Science Magazine in the list of the "top science breakthroughs of 2024". This discovery is the only entry from the field of physics on the prestigious list, which is led by advances in HIV medicine and also includes the landing of a space rocket.
Altermagnetism was proposed a couple of years ago in a series of articles by Libor Šmejkal, now a group leader at the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute for the Chemical Physics of Solids, and colleagues from Prague and Mainz. Their initial prediction in 2018 of an unconventional anomalous Hall effect and a complex compensated spin density in direct and momentum space electronic structures paved the way for their systematic spin-symmetry classification in 2021. This classification uncovered altermagnets as a new class of magnets. In altermagnets (example shown in the image), not only the spin polarisation but also the spatial orientation of the adjacent magnetic atoms alternates.
In 2024, researchers published experimental observations of altermagnetism in MnTe and CrSb using momentum-space photoemission spectroscopy at large synchrotron facilities. These experiments were guided by the theoretical work of Libor Šmejkal and his collaborators.
Further reading:
L. Šmejkal et al., Science Adv. 6, 23 (2020)
I. I. Mazin et al., PNAS 118, 42 (2021)
L. Šmejkal, J. Sinova, and T. Jungwirth, Phys. Rev. X 12, 031042 (2022)
J. Krempaský, L. Šmejkal, S. W. D'Souza, et al., Nature 626, 517 (2024)
S. Reimers et al., Nat. Commun. 15, 2116 (2024)
weiterlesenAltermagnetism was proposed a couple of years ago in a series of articles by Libor Šmejkal, now a group leader at the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute for the Chemical Physics of Solids, and colleagues from Prague and Mainz. Their initial prediction in 2018 of an unconventional anomalous Hall effect and a complex compensated spin density in direct and momentum space electronic structures paved the way for their systematic spin-symmetry classification in 2021. This classification uncovered altermagnets as a new class of magnets. In altermagnets (example shown in the image), not only the spin polarisation but also the spatial orientation of the adjacent magnetic atoms alternates.
In 2024, researchers published experimental observations of altermagnetism in MnTe and CrSb using momentum-space photoemission spectroscopy at large synchrotron facilities. These experiments were guided by the theoretical work of Libor Šmejkal and his collaborators.
Further reading:
L. Šmejkal et al., Science Adv. 6, 23 (2020)
I. I. Mazin et al., PNAS 118, 42 (2021)
L. Šmejkal, J. Sinova, and T. Jungwirth, Phys. Rev. X 12, 031042 (2022)
J. Krempaský, L. Šmejkal, S. W. D'Souza, et al., Nature 626, 517 (2024)
S. Reimers et al., Nat. Commun. 15, 2116 (2024)