Highlights
Publication Highlights
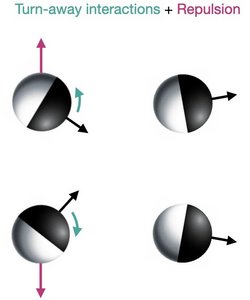
Moving together despite turning away
Self-propelled agents such as birds, cells, and active colloidal particles often move collectively in flocks. In the paradigmatic Vicsek model, flocking emerges due to alignment interactions between the active agents, which align much in the same way as spins do. Suchismita Das, Matteo Ciarchi, Ricard Alert of the Max Planck Institute for the Physics of Complex Systems and their collaborators have now discovered that flocking can emerge even if the agents turn away from each other.
The researchers made this surprising discovery in experiments with self-propelled colloidal particles that repel more strongly in their front half than in their rear half, in such a way that they turn away from each other. They then used simulations and two types of kinetic theory to explain how these particles end up flocking. Their theory revealed that repulsion between the particles is key: When two particles interact, repulsion pushes them apart before they can turn away too much, thus producing effective alignment, as shown in the figure. This crucial role of repulsion is surprising as repulsion is not even an ingredient in the paradigmatic models of flocking, such as the Vicsek model, where collective motion emerges just from alignment interactions between particle orientations. The new work also showed that, via repulsion, the particles can form flocking crystals, which are active counterparts of Wigner crystals formed through electrostatic repulsion in electron gases.
In conclusion, these active particles move in the same direction as a compromise between turning away from left and right neighbors. This mechanism of flocking could potentially be relevant for certain cells, which also turn away from each other upon collision via a process known as contact inhibition of locomotion. Whether these findings can explain how cells flock remains an open question for future work.
Suchismita Das, Matteo Ciarchi, Ziqi Zhou, Jing Yan, Jie Zhang, and Ricard Alert, Phys. Rev. X 14, 031008 (2024)
Read moreThe researchers made this surprising discovery in experiments with self-propelled colloidal particles that repel more strongly in their front half than in their rear half, in such a way that they turn away from each other. They then used simulations and two types of kinetic theory to explain how these particles end up flocking. Their theory revealed that repulsion between the particles is key: When two particles interact, repulsion pushes them apart before they can turn away too much, thus producing effective alignment, as shown in the figure. This crucial role of repulsion is surprising as repulsion is not even an ingredient in the paradigmatic models of flocking, such as the Vicsek model, where collective motion emerges just from alignment interactions between particle orientations. The new work also showed that, via repulsion, the particles can form flocking crystals, which are active counterparts of Wigner crystals formed through electrostatic repulsion in electron gases.
In conclusion, these active particles move in the same direction as a compromise between turning away from left and right neighbors. This mechanism of flocking could potentially be relevant for certain cells, which also turn away from each other upon collision via a process known as contact inhibition of locomotion. Whether these findings can explain how cells flock remains an open question for future work.
Suchismita Das, Matteo Ciarchi, Ziqi Zhou, Jing Yan, Jie Zhang, and Ricard Alert, Phys. Rev. X 14, 031008 (2024)
Awards and Honors
Prof. Matthieu Wyart awarded the "Physik Preis Dresden 2024"
On 18 June 2024, the French physicist Prof. Matthieu Wyart (EPFL, École Polytechnique Fédérale de Lausanne) was awarded the Physik Preis Dresden 2024. The theoretical physicist is being honoured for his pioneering contributions to various problems of complex systems, in particular the theory of financial markets, the physics of disordered and glassy systems as well as the theory of neural networks and machine learning. The Physik Preis Dresden is awarded annually jointly by the Dresden University of Technology and the Max Planck Institute for the Physics of Complex Systems (MPI-PKS).
Matthieu Wyart completed his PhD in Paris in 2005, where he worked together with J.-P. Bouchaud. During this time, he developed a model of price response functions in electronic markets, which became a standard in the industry. In the field of physics of disordered systems, he made an important breakthrough very early on by explaining how the surplus of soft modes in closely-packed systems of particles is controlled by their disordered geometry. This work elegantly solved the long-standing problem of the origin of the so-called boson peak in glasses with repulsive interactions. As a postdoc, he moved to Harvard and then Princeton before becoming an assistant and associate professor at New York University. He has been a professor at EPF Lausanne since 2015.
In recent years, Matthieu Wyart's original approaches and way of reasoning have had a strong impact and brought new insights into the physics of disordered systems. More recently, he has made significant contributions to the problem of the nature of the glass transition. In particular, his work suggests that increasing local energy barriers control the slowing down of dynamics in supercooled liquids, as opposed to co-operative effects.
The numerous original approaches to solving problems in different fields and disciplines are testimony to his extraordinary scientific excellence. In recognition of his outstanding contributions to the physics of complex and disordered systems, the Dean of the Faculty of Physics at Dresden University of Technology, Prof. Gesche Pospiech, together with Prof. Frank Jülicher, Director at the MPI-PKS, awarded the Physik Preis Dresden 2024 to Matthieu Wyart on 18 June 2024 as part of the Physics Colloquium.
The Physik Preis Dresden, endowed with 5,000 euros, was founded in 2015 by the Dresden physicist Prof Peter Fulde (1936-2024), the founding director of the MPI-PKS, and has been awarded annually to renowned scientists since 2017. The award winners are selected by a joint commission of the Dresden University of Technology and the MPI-PKS. In addition to the central criterion of scientific excellence, it is particularly important for the decision that the work of the award winners is of particular importance for the cooperation between the two DRESDEN-concept partners MPI-PKS and TUD and that their connection has been further strengthened in the long term.
Read morePublication Highlights
Quantum skyrmion Hall effect
The framework of the quantum Hall effect has been extended to a framework of a quantum skyrmion Hall effect by Ashley Cook of the Max Planck Institute for the Physics of Complex Systems and the Max Planck Institute for Chemical Physics of Solids, by generalizing the notion of a particle to include compactified p-dimensional charged objects. This is consistent with three sets of topologically non-trivial phases of matter previously discovered by Cook and collaborators: the topological skyrmion phases of matter, the multiplicative topological phases of matter, and the finite-size topological phases of matter. These findings indicate that topological states of D-dimensions can persist after compactification and yield previously unidentified generalizations of particles, a finding of relevance to many areas of physics, and particularly string theory, with great potential for rapid experimental confirmation.
Ashley Cook, Phys. Rev. B 109, 155123 (2024)
Read moreAshley Cook, Phys. Rev. B 109, 155123 (2024)
Publication Highlights
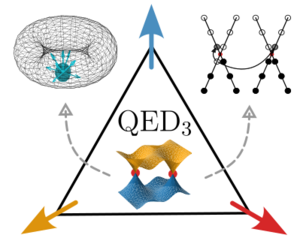
Quantum Electrodynamics in 2+1 Dimensions as the Organising Principle of a Triangular Lattice Antiferromagnet
Quantum electrodynamics (QED) is the fundamental theory that describes the interactions between electrons and photons. Its success has led some to wonder whether quantum field theories, like QED, can describe quasiparticles in a solid. These collective excitations include phonons, which describe lattice vibrations, and magnons, which are waves in a magnetic material, but might also be of a more exotic nature. In a recent study, Alexander Wietek of the Max Planck Institute for the Physics of Complex Systems and his collaborators show that QED in two spatial dimensions can be observed in frustrated antiferromagnets.
An antiferromagnet is a material in which neighbouring electron spins in the crystal lattice would like to point in opposite directions. However, in certain geometries, such as a triangular lattice, it is impossible to have all neighbouring spins align in precisely the opposite way. This is called geometric frustration and can lead to strong disorder in the system. This disorder is not featureless, however. In fact, it is shown that the quasiparticles of such a spin soup, known as a quantum spin liquid, are related one-to-one to excitations of QED. Importantly, even the elusive magnetic monopoles, among a wide variety of other particle-hole excitations, are observed.
The precise understanding of the spin-liquid state with magnetic monopoles as elementary excitations is a key step to discovering these exotic quasiparticles in antiferromagnetic materials. It is unlikely that the founders of QED would have predicted such a surprising emergence in condensed matter.
Alexander Wietek, Sylvain Capponi, and Andreas M. Läuchli, Phys. Rev. X 14, 021010 (2024)
Selected for a Viewpoint in Physics.
Read moreAn antiferromagnet is a material in which neighbouring electron spins in the crystal lattice would like to point in opposite directions. However, in certain geometries, such as a triangular lattice, it is impossible to have all neighbouring spins align in precisely the opposite way. This is called geometric frustration and can lead to strong disorder in the system. This disorder is not featureless, however. In fact, it is shown that the quasiparticles of such a spin soup, known as a quantum spin liquid, are related one-to-one to excitations of QED. Importantly, even the elusive magnetic monopoles, among a wide variety of other particle-hole excitations, are observed.
The precise understanding of the spin-liquid state with magnetic monopoles as elementary excitations is a key step to discovering these exotic quasiparticles in antiferromagnetic materials. It is unlikely that the founders of QED would have predicted such a surprising emergence in condensed matter.
Alexander Wietek, Sylvain Capponi, and Andreas M. Läuchli, Phys. Rev. X 14, 021010 (2024)
Selected for a Viewpoint in Physics.
Publication Highlights
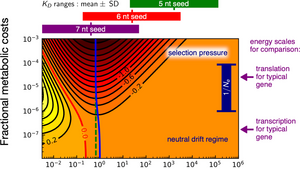
Bioenergetic costs and the evolution of noise regulation by microRNAs
MicroRNAs (miRNAs) are short strands of genetic material that regulate various cellular functions and developmental processes. One of the regulatory functions of miRNAs is noise control that confers robustness in gene expression. The interaction with their target messenger RNA (mRNA) requires a specific binding sequence of 6-8 nucleotide pairs in length. There are a variety of open questions about the evolution of miRNA regulation regarding their functional efficiency and binding specificity.
Efe Ilker of the Max Planck Institute for the Physics of Complex Systems and Michael Hinczewski (Case Western Reserve University) show that this regulation incurs a steep energetic price, so that natural selection may have driven such systems towards greater energy efficiency. This involves tuning the interaction strength between miRNAs and their target messenger RNAs, which is controlled by the length of a miRNA seed region that pairs with a complementary region on the target. They show for the first time that microRNAs lie in an evolutionary sweet spot that may explain why 7 nucleotide pair interactions are prevalent: sequences that are much longer or shorter would not have the right binding properties to reduce noise optimally. To achieve this, they develop a stochastic model of miRNA noise regulation, coupled with a detailed analysis of the associated metabolic costs and binding free energies for a wide range of miRNA seeds. Moreover, the behaviour of the optimal miRNA network mimicks the best possible linear noise filter, a classic concept in engineered communication systems. These results illustrate how selective pressure toward metabolic efficiency has potentially shaped a crucial regulatory pathway in eukaryotes.
Efe Ilker and Michael Hinczewski, Proc. Natl. Acad. Sci. USA 121, e2308796121 (2024)
Read moreEfe Ilker of the Max Planck Institute for the Physics of Complex Systems and Michael Hinczewski (Case Western Reserve University) show that this regulation incurs a steep energetic price, so that natural selection may have driven such systems towards greater energy efficiency. This involves tuning the interaction strength between miRNAs and their target messenger RNAs, which is controlled by the length of a miRNA seed region that pairs with a complementary region on the target. They show for the first time that microRNAs lie in an evolutionary sweet spot that may explain why 7 nucleotide pair interactions are prevalent: sequences that are much longer or shorter would not have the right binding properties to reduce noise optimally. To achieve this, they develop a stochastic model of miRNA noise regulation, coupled with a detailed analysis of the associated metabolic costs and binding free energies for a wide range of miRNA seeds. Moreover, the behaviour of the optimal miRNA network mimicks the best possible linear noise filter, a classic concept in engineered communication systems. These results illustrate how selective pressure toward metabolic efficiency has potentially shaped a crucial regulatory pathway in eukaryotes.
Efe Ilker and Michael Hinczewski, Proc. Natl. Acad. Sci. USA 121, e2308796121 (2024)
Publication Highlights
Characterising the gait of swimming microorganisms
The survival strategies of Escherichia Coli are controlled by their run-and-tumble "gait". While much is known about the molecular mechanisms of the bacterial motor, quantifying the motion of these microorganisms in three dimensions has remained challenging. Christina Kurzthaler of the Max Planck Institute for the Physics of Complex Systems and her collaborators have now proposed a high-throughput method, using differential dynamic microscopy and a renewal theory, for measuring the run-and-tumble behavior of a population of E. Coli cells. Besides providing a full spatiotemporal characterisation of their swimming gait, this new method allowed relating, for the first time, molecular properties of the motor to the dynamics of engineered E. coli cells. It therefore lays the foundation for future studies on gait-related phenomena in different microorganisms and has the potential of becoming a standard tool for rapidly determining motility parameters of swimming cells.
More details can be found in a press release (PDF).
C. Kurzthaler*, Y. Zhao*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, J. Tailleur, and V. A. Martinez, Phys. Rev. Lett. 132, 038302 (2024)
Y. Zhao*, C. Kurzthaler*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, V. A. Martinez, and J. Tailleur, Phys. Rev. E 109, 014612 (2024)
Selected for a Synposis in Physics.
Read moreMore details can be found in a press release (PDF).
C. Kurzthaler*, Y. Zhao*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, J. Tailleur, and V. A. Martinez, Phys. Rev. Lett. 132, 038302 (2024)
Y. Zhao*, C. Kurzthaler*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, V. A. Martinez, and J. Tailleur, Phys. Rev. E 109, 014612 (2024)
Selected for a Synposis in Physics.
Publication Highlights
Exotic fractons constraining electron motion to one dimension
Fractons are the latest addition to the set of exotic quasiparticles in condensed matter, and models exhibiting fracton phenomenology are highly sought after. Alexander Wietek of the Max Planck Institute for the Physics of Complex Systems and his collaborators have now proposed a model that shows this phenomenology. They studied a simple "doped" Ising magnet on the two-dimensional honeycomb lattice with anisotropic Ising couplings that exhibits a dipolar symmetry. This peculiar property leads to the complete localization of one hole, whereas a pair of two holes is localized only in one spatial dimension. The emergent dipole symmetry is found to be remarkably precise, being present up to the 15th order of perturbation theory and to numerically accurate precision away from the perturbative limit. The proposed model captures the very essence of subdimensional mobility constraints and could become a prime example of how new and exotic fracton-like quasiparticles can be implemented in a condensed matter setting.
Sambuddha Sanyal, Alexander Wietek, and John Sous, Phys. Rev. Lett. 132, 016701 (2024)
Read moreSambuddha Sanyal, Alexander Wietek, and John Sous, Phys. Rev. Lett. 132, 016701 (2024)
Publication Highlights
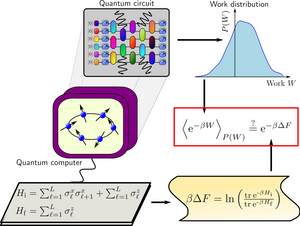
Using quantum computers to test Jarzynski’s equality for many interacting particles
Statistical mechanics is a branch of physics that uses statistical and probabilistic methods to understand the behaviour of large numbers of microscopic particles, such as atoms and molecules, in a system. Instead of focusing on the individual motion of each particle, statistical mechanics analyses the collective properties of the system. It provides a bridge between the microscopic world of particles and the macroscopic world that we can observe, explaining phenomena like the behaviour of liquids and gases, phase transitions, and the thermodynamic properties of materials. Through the statistical distribution of particle properties, such as energy and velocity, statistical mechanics helps us make predictions about how physical systems behave on a larger scale, contributing to our understanding of fundamental principles in physics and chemistry.
One of the most remarkable relations in statistical mechanics is Jarzynski's equality, connecting the irreversible work performed in an arbitrary thermodynamic process with the energy and entropy of the system in thermodynamic equilibrium. Because the system is free to leave the equilibrium state during its evolution, Jarzynski’s equality is a prime example of how equilibrium physics can constrain the outcome of nonequilibrium processes. Remarkably, the familiar Second Law of Thermodynamics – a fundamental principle of physics – follows directly from Jarzynski’s equality. The Second Law is a statement about the average properties of particles in a system undergoing a thermodynamic process, and postulates that heat always flows spontaneously from hotter to colder regions of the system. Intriguingly, Jarzynski’s equality shows that this fundamental law of Thermodynamics can be “violated” in individual realizations of a process (but never on average!).
Despite its fundamental importance, experimental tests of Jarzynski’s equality for classical and quantum systems are extremely challenging, since they require complete control in manipulating and measuring the system. Even more so, a test for many quantum interacting particles was until recently completely missing.
In a new joint study, an international team from the Max Planck Institute for the Physics of Complex Systems, the University of California at Berkeley, the Lawrence Berkeley National Laboratory, the German Cluster of Excellence ML4Q and the Universities of Cologne, Bonn, and Sofia identified quantum computers as a natural platform to test the validity of Jarzynski’s equality for many interacting quantum particles. (A quantum computer is a computing device that uses the principles of Quantum Mechanics to perform certain types of calculations at speeds and efficiency levels that are unattainable by classical computers. Quantum computers use quantum bits, or qubits, as the basic unit of information. Hence, any quantum computer is, at its core, a system of interacting quantum particles.) The researchers used the quantum bits of the quantum processor to simulate the behaviour of many quantum particles undergoing nonequilibrium processes, as is desired for an experimental verification of Jarzynski’s equality. They tested this fundamental principle of nature on multiple devices and using different quantum computing platforms. To their surprise, they found that the agreement between theory and quantum simulation was more accurate than originally expected due to the presence of computational errors, which are omnipresent in current quantum computers. The results demonstrate a direct link between certain types of errors that can occur in quantum computations and violations of Jarzynski’s equality, revealing a fascinating connection between quantum computing technology and this fundamental principle of physics.
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, and Marin Bukov, Physical Review X 13, 041023 (2023)
Read moreOne of the most remarkable relations in statistical mechanics is Jarzynski's equality, connecting the irreversible work performed in an arbitrary thermodynamic process with the energy and entropy of the system in thermodynamic equilibrium. Because the system is free to leave the equilibrium state during its evolution, Jarzynski’s equality is a prime example of how equilibrium physics can constrain the outcome of nonequilibrium processes. Remarkably, the familiar Second Law of Thermodynamics – a fundamental principle of physics – follows directly from Jarzynski’s equality. The Second Law is a statement about the average properties of particles in a system undergoing a thermodynamic process, and postulates that heat always flows spontaneously from hotter to colder regions of the system. Intriguingly, Jarzynski’s equality shows that this fundamental law of Thermodynamics can be “violated” in individual realizations of a process (but never on average!).
Despite its fundamental importance, experimental tests of Jarzynski’s equality for classical and quantum systems are extremely challenging, since they require complete control in manipulating and measuring the system. Even more so, a test for many quantum interacting particles was until recently completely missing.
In a new joint study, an international team from the Max Planck Institute for the Physics of Complex Systems, the University of California at Berkeley, the Lawrence Berkeley National Laboratory, the German Cluster of Excellence ML4Q and the Universities of Cologne, Bonn, and Sofia identified quantum computers as a natural platform to test the validity of Jarzynski’s equality for many interacting quantum particles. (A quantum computer is a computing device that uses the principles of Quantum Mechanics to perform certain types of calculations at speeds and efficiency levels that are unattainable by classical computers. Quantum computers use quantum bits, or qubits, as the basic unit of information. Hence, any quantum computer is, at its core, a system of interacting quantum particles.) The researchers used the quantum bits of the quantum processor to simulate the behaviour of many quantum particles undergoing nonequilibrium processes, as is desired for an experimental verification of Jarzynski’s equality. They tested this fundamental principle of nature on multiple devices and using different quantum computing platforms. To their surprise, they found that the agreement between theory and quantum simulation was more accurate than originally expected due to the presence of computational errors, which are omnipresent in current quantum computers. The results demonstrate a direct link between certain types of errors that can occur in quantum computations and violations of Jarzynski’s equality, revealing a fascinating connection between quantum computing technology and this fundamental principle of physics.
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, and Marin Bukov, Physical Review X 13, 041023 (2023)
Publication Highlights
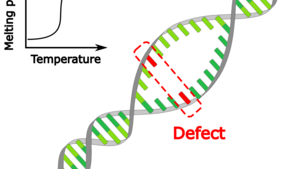
Investigating the impact of a defect basepair on DNA melting
As temperature is increased, the two strands of DNA separate. This DNA melting is described by a powerful model of statistical physics, the Poland–Scheraga model. It is exactly solvable for homogeneous DNA (with only one type of basepairs), and predicts a first-order phase transition.
Arthur Genthon of the Max Planck Institute for the Physics of Complex Systems, Albertas Dvirnas and Tobias Ambjörnsson (Lund University, Sweden) have now derived an exact equilibrium solution of an extended Poland–Scheraga model that describes DNA with a defect site that could, for instance, result from DNA basepair mismatching, cross-linking, or the chemical modifications from attaching fluorescent labels, such as fluorescent-quencher pairs, to DNA. This defect was characterized by a change in the Watson–Crick basepair energy of the defect basepair, and in the associated two stacking (nearest-neighbour) energies for the defect compared to the remaining parts of the DNA. The exact solution yields the probability that the defect basepair and its neighbors are separated at different temperatures. In particular, the authors investigated the impact of the defect on the phase transition, and the number of base pairs away from the defect at which its impact is felt. This work has implications for studies in which fluorophore-quencher pairs are used to analyse single-basepair fluctuations of designed DNA molecules.
Arthur Genthon, Albertas Dvirnas, and Tobias Ambjörnsson, J, Chem. Phys. 159, 145102 (2023)
Read moreArthur Genthon of the Max Planck Institute for the Physics of Complex Systems, Albertas Dvirnas and Tobias Ambjörnsson (Lund University, Sweden) have now derived an exact equilibrium solution of an extended Poland–Scheraga model that describes DNA with a defect site that could, for instance, result from DNA basepair mismatching, cross-linking, or the chemical modifications from attaching fluorescent labels, such as fluorescent-quencher pairs, to DNA. This defect was characterized by a change in the Watson–Crick basepair energy of the defect basepair, and in the associated two stacking (nearest-neighbour) energies for the defect compared to the remaining parts of the DNA. The exact solution yields the probability that the defect basepair and its neighbors are separated at different temperatures. In particular, the authors investigated the impact of the defect on the phase transition, and the number of base pairs away from the defect at which its impact is felt. This work has implications for studies in which fluorophore-quencher pairs are used to analyse single-basepair fluctuations of designed DNA molecules.
Arthur Genthon, Albertas Dvirnas, and Tobias Ambjörnsson, J, Chem. Phys. 159, 145102 (2023)
Publication Highlights
A Quantum Root of Time for Interacting Systems
In 1983, the two physicists Page and Wootters postulated a timeless entangled quantum state of the universe in which time emerges for a subsystem in relation to the rest of the universe. This radical perspective of one quantum system serving as the other’s temporal reference resembles our traditional use of celestial bodies’ relative motion to
track time. However, a vital piece has been missing: the inevitable interaction of physical systems.
Forty years later, Sebastian Gemsheim and Jan M. Rost from the Max Planck Institute for the Physics of Complex Systems have finally shown how a static global state, a solution of the time-independent Schrödinger equation, gives rise to the time-dependent Schrödinger equation for the state of the subsystem once it is separated from its environment to which it retains arbitrary static couplings. Exposing a twofold role, the environment additionally provides a time-dependent effective potential governing the system dynamics, which is intricately encoded in the entanglement of the global state. Since no approximation is required, intriguing applications beyond the question of time are within reach for heavily entangled quantum systems, which are elusive but relevant for processing quantum information.
Sebastian Gemsheim and Jan M. Rost, Phys. Rev. Lett. 131, 140202 (2023)
Read moreForty years later, Sebastian Gemsheim and Jan M. Rost from the Max Planck Institute for the Physics of Complex Systems have finally shown how a static global state, a solution of the time-independent Schrödinger equation, gives rise to the time-dependent Schrödinger equation for the state of the subsystem once it is separated from its environment to which it retains arbitrary static couplings. Exposing a twofold role, the environment additionally provides a time-dependent effective potential governing the system dynamics, which is intricately encoded in the entanglement of the global state. Since no approximation is required, intriguing applications beyond the question of time are within reach for heavily entangled quantum systems, which are elusive but relevant for processing quantum information.
Sebastian Gemsheim and Jan M. Rost, Phys. Rev. Lett. 131, 140202 (2023)