Research
Research
A Rydberg atom is an atom in which one electron has been excited to a very high principal quantum number. Such excited states have exaggerated properties: long (micro - to - millisecond) lifetimes, enormous (nano - to - micrometer) sizes, and strong (MHz-GHz) interactions, either at very long range with other Rydberg atoms or over shorter range with ground state atoms. Thanks to these properties, Rydberg atoms form a bridge between the microscopic world (atoms, electrons, and molecules) and the mesoscopic world of micrometer length scales, optical lattices, Bose-Einstein condensates, and structured or amorphous condensed matter. They combine the exquisite control and manipulation achievable with ultracold atoms with the flexibility and strong interactions of more complicated systems.
We are interested in exploring theoretically the structure and dynamics of Rydberg matter -- encompassing intera interacting Rydberg atoms, ground state atoms immersed within the electronic wave function of a Rydberg atom, Rydberg molecules, and Rydberg quasiparticles (excitons, polarons, etc).
Via the study of Rydberg physics we can answer fundamental questions about...
- Atomic structure / molecular and chemical physics / nanoclusters
- Low energy collisions / scattering / short- and long-range interactions
- Control and manipulation of ultracold gases
...and raise new questions about...
- Localization / transport / topology
- Highly correlated systems
- Quantum scars / quantum chaos / semiclassical dynamics
- Quantum simulators
- Transition from few to many body physics
Due to their flexibility, Rydberg atoms shed insight into all these (and more!) theoretical inquiries, stimulated by rapid experimental progress in Rydberg atoms, atomic tweezers, optical lattices, ultracold condensates, and so on. Parallel systems, which bear interesting similarities and connections to Rydberg matter, include highly correlated atomic negative ions, quantum dots, electron-hole pairs, and more.
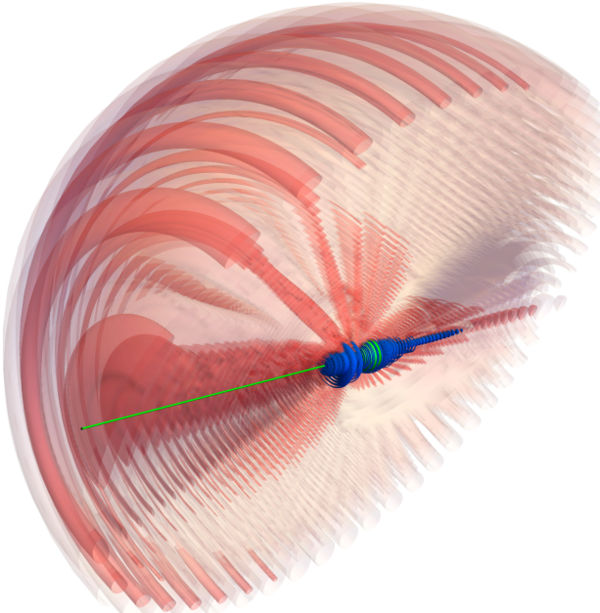
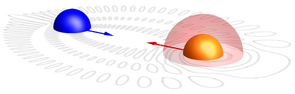
The electronic Rydberg wave function of a "butterfly" molecule, another creature in our quantum zoo. This wave function is highly polar and traps a ground state atom between two electronic density maxima on the internuclear axis (green).
EXOTIC RYDBERG MOLECULES
Rydberg molecules - such as the trilobite and butterfly molecules - are comprised of a Rydberg atom and a ground state atom. In a recent paper we predicted a new "dragonfly" molecule whose energy spectrum conforms to a certain mise en abyme: nested within successive levels of the infinite electronic Rydberg series lie several finite vibrational Rydberg series. These intertwined series arise from Coulomb potentials in the electronic and nuclear degrees of freedom. The emergence of nuclear Coulomb interaction in a Rydberg molecule is surprising because it is otherwise found only in a heavy Bohr atom, consisting of a cation and an anion.
We establish a connection between heavy Bohr atoms and Rydberg molecules via a dressed ion-pair model. In this new perspective, the low-energy scattering of the Rydberg electron off of the ground state atom dresses the neutral atom with a fractional negative charge. Coulomb forces between this dressed anion and the Rydberg cation lead to the formation of Rydberg molecules. In the class of Rydberg molecules we predict, this charge is nearly independent of the internuclear distance, yielding a Coulombic potential.
Although this property and the effective ion-pair binding mechanism are very unusual, these molecules need not be: our work shows that these are generic, and can be formed from a Rydberg atom and any neutral polarizable object, and we look forward to continuing investigations along this direction.
This work was a collaboration with Panos Giannakeas and Jan Michael Rost of MPI-PKS and Francis Robicheaux of Purdue University.
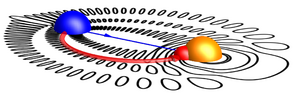
Above: The surprising mise en abyme of a Rydberg molecule. credit: Panos Giannakeas
Below: The standard "trilobite" molecule and our re-interpretation as a dressed negative ion pair. credit: P. Giannakeas, Matthew T. Eiles, F. Robicheaux, and Jan M. Rost Phys. Rev. Lett. 125, 123401 (2020)
EXCITON DELOCALIZATION IN RYDBERG GASES
A "frozen Rydberg gas" has many characteristics which make it ideal for investigation. Two beneficial properties for us are the long-range interactions between particles due to the huge dipole moments of Rydberg atoms, and the near absence of motion due to available ultracold temperatures and relevant time scales. Such gases are routinely studied in the laboratory and can be either completely randomly arranged, as in a thermal vapor, or structured, as in a tweezer array or optical lattice. Curiously, the interaction between Rydberg atoms can even lead to additional crystalline structure via the Rydberg blockade.
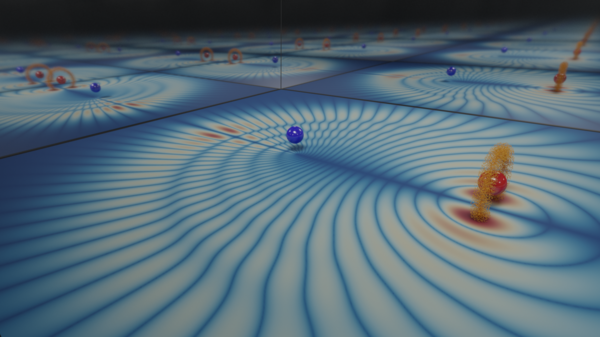
In recent work we discovered that the long-range dipole-dipole interaction can create delocalized excitonic states due to the exchange of excitation between Rydberg atoms. We showed that even in a random gas many of the single-exciton eigenstates are surprisingly delocalized, composed of roughly one quarter of the participating atoms. Two different types of eigenstates exist in the gas, shown on the right: one (panel a) which stems from strongly-interacting clusters, resulting in localized states (panel c), and one (panel b) which extends over large delocalized networks of atoms (panel d). These two types of states can be excited and distinguished by appropriately tuned microwave pulses, and their relative contributions can be modified by the Rydberg blockade and the choice of microwave parameters.
In the future we will explore how the degeneracy of Rydberg sublevels and the spin-orbit fine structure of the Rydberg states modify these localization properties, and how to further study and manipulate them in experiment.
This work was a collaboration with Ghassan Abumwis and Alex Eisfeld of MPI-PKS.
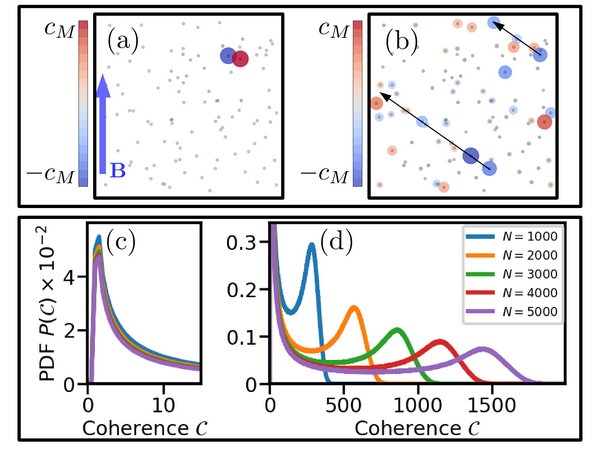
Cartoons of the Rydberg gas showing cluster states (a) and extended states (b). We quantify the extent of delocalization via a coherence measure, which reveals the presence of cluster states of closeby two, three,... atoms (c) as well as extended networks of long-range interacting atoms (d). The size of these extended states grows linearly with the number of atoms. credit: G. Abumwis, Matthew T. Eiles, and Alexander Eisfeld. Phys. Rev. Lett. 124, 193401 (2020).
RYDBERG COMPOSITES
In collaboration with Andrew Hunter, Jan Michael Rost, and Alex Eisfeld of MPI-PKS, we have worked to extend the concept of a Rydberg molecule to that of a "Rydberg composite" by greatly increasing the number of atoms immersed in the Rydberg electron's wave function. Recent advancements in both the densities achievable in ultracold experiments and the ability of researchers to arrange them into regular grids or shapes motivate this study. These kinds of arrangements lead to a variety of interesting prospects as they introduces these concepts from Rydberg, and more broadly, AMO physics, into a new context in solid-state or condensed matter physics. For example, we have studied two-dimensional composites where the scatterer atoms are arranged in a plane surrounding the core of a Rydberg atom, and periodic one-dimensional composites where the scatterers are placed in a ring around the Rydberg core.
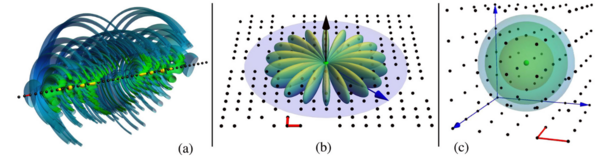
Rydberg composites in one-, two-, and three-dimensional lattices.
In general, this composite system is a rich and flexible platform for introducing and uniting concepts from the typically disparate fields of atomic few body physics and solid-state or condensed matter physics, hinging on the interplay between the geometry and structure (lattice spacing, dimensionality, filling statistics) of the array of atoms and the nature of the Rydberg electron (high degeneracy, specific density of states, structured eigenstates). We have plans to utilize it to study a range of connected topics related to correlation, transport, localization, topology, and more...


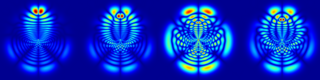
Above: a gallery of electronic wave functions in ordered and disordered two-dimensional Rydberg composites. Structured wave functions obeying the lattice symmetries, scarred wave functions in chaotic regimes, and the adaptation of the wave functions to new symmetry classes in the large-density scatterer regime are all apparent. credit: Andrew L. Hunter, Matthew T. Eiles, Alexander Eisfeld, and Jan M. Rost Phys. Rev. X 10, 031046 (2020)
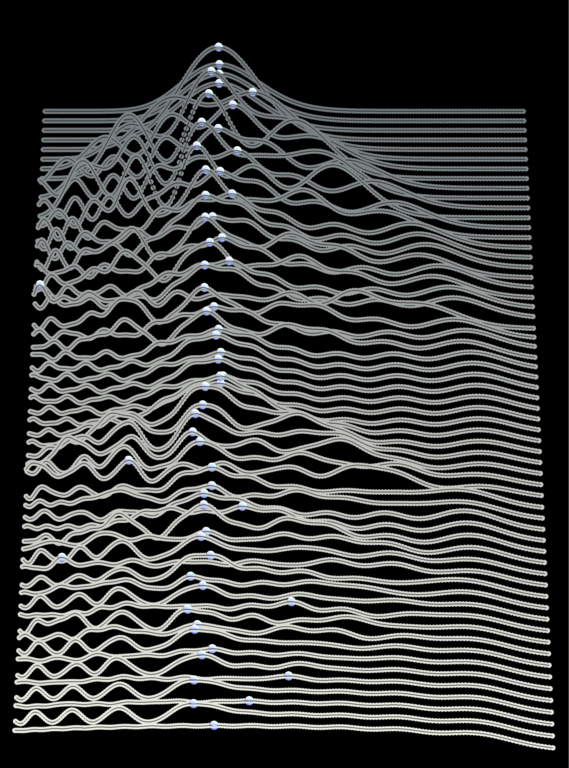
Below: eigenspectra of a ring Rydberg composite as a function of ring radius (horizontal axis) and number of scatterers (vertical axis). credit: Matthew T. Eiles, Andrew L. Hunter, and Jan M. Rost J. Phys. B: At. Mol. Opt. Phys. 53 054001 (2020)