
Research
Discovery of a Floquet topological phase transition (2008)
Topology is one of the key concepts in modern condensed matter physics. It was believed that ``topology is robust against perturbation” and is something that is fixed when a material is synthesized. Actually, there is a way to cheat this. In 2009, we found the first example of the so-called Floquet topological insulator. We showed that the Berry curvature, Chern number, and the chiral edge state in almost ANY two dimensional multi-band systems can be controlled or induced by external time periodic fields such as laser. The key idea is that electrons become photo-dressed. They are described by Floquet states, a temporal analogue of Bloch states, and the topology of the quasi-energy bands can be changed as a function of the laser intensity, polarization and frequency. This idea is not limited to an electron-laser system, but can be universally applied to various physical systems, such as electron-coherent phonon, photon-optical wave guide, cold atom-optical lattice etc. In solid state physics, the concept of Floquet states already existed from the 70’s, but our works is pushing it to the frontline by attracting researchers from various backgrounds such as topological insulators , laser physics, nonequilibrium statistical mechanics, helping the field to accelerate its progress.
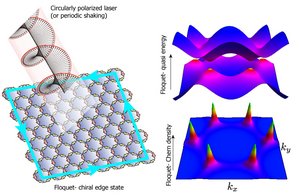
Figure: (Left) Honeycomb lattice in circularly polarized laser becomes a Floquet Chern insulator.
(Right) The Floquet quasi-energy in the high frequency limit shows a gap opening at the Dirac points. This leads to the emergence of the Chern density. If the lower Floquet band is fully occupied, the Floquet-Chern number would be one.
Nonequilibrium theory of strongly correlated superconductors
We have developed a numerical method to calculate the quantum dynamics of unconventional superconductors (high Tc cuprates and possibly iron pnictides) by combining the quantum kinetic equation with the nonequilibrium FLEX method. This method is complementary to the nonequilibrium dynamical mean field theory (Aoki, Oka, et al. RMP’14) and is able to treat nonlocal correlation such as the paramagnetic fluctuation considered responsible as the pairing glue (at least in the over doped region). This method still needs refinement. After completing this method, we will apply it to study nonlinear device application and ultrafast phenomena in unconventional superconductors.
Ultrafast spintronics (control of spin and spin current by laser)
With Shintaro Takayoshi and Masahiro Sato, we initiated a collaboration to study ultrafast dynamics in quantum magnets. While many of the well studied dynamical processes in magnets such as domain wall motion and skyrmion dynamics can be described within the semiclassical framework (LLG equation), if we want to study ultrafast dynamics (= picosecond time scale), it becomes important to start from a microscopic and quantum mechanical theory. We tried applying tricks such as the Floquet theory that we learned from our study of electron systems to models of quantum spins. One idea which may be experimentaly relevant is the laser induced magnetization curve . In a more recent ariticle, we have shown that it is possible to generate spin current in multiferrioc materials using laser.
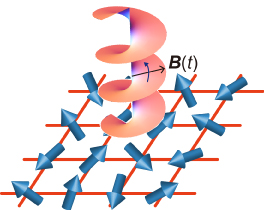
Figure: One can induce a strong "effective magnetic field" by applying a rotating magnetic field to a quantum magnet. The strength of the effective field equals the photon-energy of the laser, and can be easily around the range of 100 teslas if a THz laser is used. We can use this field to realize the "laser induced magnetization curve" without using magnetic fields.
Schwinger effect in correlated electron systems and its first observation (2003 - 2015)
In high energy physics, there is a branch called nonlinear quantum field theory (or strong field physics), where nonlinear processes and the breakdown of the quantum vacuum in strong electro-magnetic fields are being studied. This area is an old one that partially started from the study by Heisenberg and Euler in 1936, who predicted nonlinear optical responce of the vacuum. In stronger fields, the QED vacuum becomes unstable against production of electron-positron pairs via quantum tunneling, and Schwinger obtained the one-loop expression of the vacuum decay rate. These processes are one of the main targets in recent pan-European laser projects such as XFEL and ELI. In addition, applications of nonlinear QFT can be found in quark-gluon plasma formation in heavy ion collision experiments as well as in magnetars (neutron star with strong magnetic fields).
The Zener tunneling in semiconductor physics is formally equivalent to the Schwinger effect. Concepts and developed techniques in high energy theory often has deep connection to those in condensed matter. For example, the framework of the Heisenberg-Euler effective Lagrangian is actually a nonadiabatic version of the Berry phase theory of polarization. One contribution we made in this field is to take into account the effect of interaction. This was lacking or incomplete in both fields. We studied the dielectric breakdown process in the Mott insulator using the Hubbard model as well as in SUSY QCD using gauge/gravity duality. The physical insights obtained in the two systems are in fact coherent with differences originating from properties of the interactions.
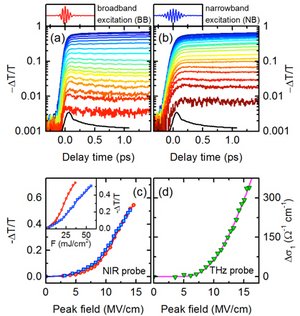
Recently, the Schwinger effect in a strongly correlated insulator was realized (the lower right panel in the figure). From a fundamental physics point of view, I think it interesting that we can mimic high energy ideas such as the Schwinger effect using a well-controlled platforms that condensed matter experiments offer.
Gauge/gravity duality applied in nonequilibrium dynamics
Nonequilibrium quantum phenomenon is an interesting subject that attracts researchers with diverse background. I was lucky enough to start collaboration with string theorists K. Hashimoto and A. Sonoda and gravity theory specialists S. Kinoshita and K. Murata. Our project is based on the usage of the gauge gravity duality that relates quantum field theories to gravitational systems in a higher dimensional space.
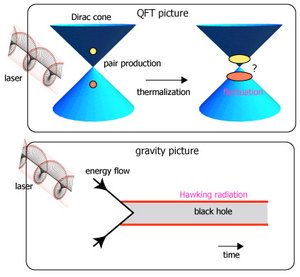
Gauge/gravity duality relates two interesting nonequilibrium phenomena. One is the excitation and relaxation process of strongly interacting particles, and the other is the black hole creation/ evaporation process (Figure). Both problems are not easy to understand because we lack reliable theoretical tools. However, by comparing both sides of the duality, and with input from experiments, we are able to obtain a coherent understanding.
The model we study is supersymmetric QCD. This is a model with three dimensional Dirac fermions and interaction mediating gluons (plus SUSY partners). We are tempted to compare the results with experiments done in solid states such as three dimensional Dirac system as well as in Weyl semimetal (and we think this is not a bad idea).
Methods for strongly correlated nonequilibrium systems
Developing reliable methods to treat nonequilibrium many-body physics is important. I have a simple strategy in doing this: “Pick the most reliable method in equilibrium and extend it to nonequilibrium”. The following is a list of methods that we have developed (thanks to my collaborators).
- Bethe ansatz + Landau-Dykhne method: This is a powerful method that enabled me to study the Schwinger effect in the 1D Hubbard model.
- Nonequilibrium continuous time QMC: A method developed with P. Werner and A. Millis.
- Nonequilibrium dynamical mean field theory for the Hubbard model (Aoki et al. RMP 2014): This was mainly developed by P. Werner, M. Eckstein and N. Tsuji. My contribution is limited.
- Nonequilibrium fluctuation exchange approximation (noneq. FLEX): I tried to develop a method to study unconventional superconductors including Hi Tc cuprates and possibly iron pnictides far from equilibrium.
- Floquet TKNN (Kubo) formula: I have extended the linear response theory to Floquet states using the two-time method. Using this formula, I predicted the laser-induced quantum Hall effect (Floquet topological insulator).
- Floquet DMFT: N. Tsuji combined the DMFT method with the Floquet theory. This is useful in studying laser-induced Mott insulator-to-metal transitions.
- Floquet + bozonization/fermionization: Nice analytical method to study periodically driven 1D quantum field theories.
- Heisenberg-Euler effective Lagrangian in gauge/gravity duality: We extended the GKP-Witten dictionary to unstable vacua. We used this method to calculate the decay rate of the hadronic vacuum in SUSY QCD against strong electromagnetic fields.