
Research
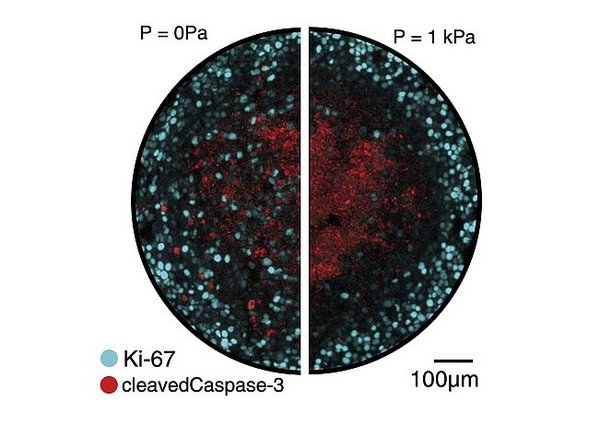
Image from F. Montel, M. Delarue, J. Elgeti, L. Malaquin, M. Basan, T. Risler, B. Cabane, D. Vignjevic, J. Prost, G. Cappello, and J-F. Joanny. PRL 107, 188102 (2011)
Stochastic tissue growth
Tissues grow by cell proliferation, which is a stochastic process. We study how the variability at the cell scale yields robust growth at the tissue scale. In one example, we ask how spatial disorder in cell growth affects tissue buckling. In another example, we study the feedback between cell proliferation and pressure in tissues.
Publications
R.G. Ramachandran, R. Alert, and P.A. Haas. Buckling by disordered growth. PRE (2024)
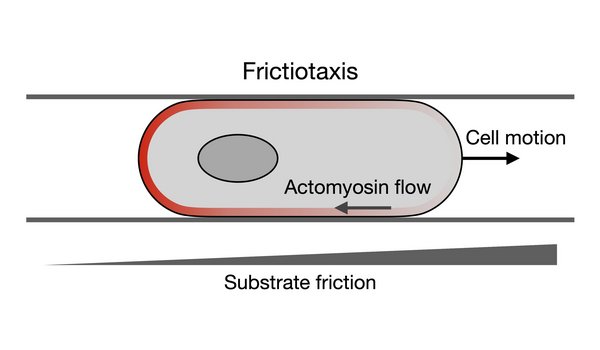
Image from A. Shellard*, K. Weißenbruch*, P.A.E. Hampshire*, N.R. Stillman, C. Dix, R. Thorogate, A. Imbert, G. Charras, R. Alert, and R. Mayor. Nat. Commun. (2025)
Guidance mechanisms for cell migration
We study how cells direct their motion to follow environmental signals. For example, we study how cells move along gradients in substrate friction — a new type of directed cell migration that we call frictiotaxis. This type of directed motion is possible even when cells do not adhere to the substrate, like is the case for amoeboid migration.
Publications
- A. Shellard*, K. Weißenbruch*, P.A.E. Hampshire*, N.R. Stillman, C. Dix, R. Thorogate, A. Imbert, G. Charras, R. Alert, and R. Mayor. Frictiotaxis underlies focal adhesion-independent durotaxis. Nat. Commun. (2025)

Image from K. Copenhagen*, R. Alert*, N.S. Wingreen, and J.W. Shaevitz. Nat. Phys. (2021)
Collective cell migration in bacterial colonies
We study how groups of bacteria migrate collectively. For example, we model colonies of motile bacteria as active fluids to understand collective behaviors such as the formation of layered aggregates and fruiting bodies. In another example, we study how propagating fronts of chemotactic bacteria manage to remain stable even when moving through porous media.
Publications
- D. Banerjee and R. Alert. Active Screws: Emergent Active Chiral Nematics of Spinning Self-Propelled Rods. arXiv (2024)
- M.E. Black*, C. Fei*, R. Alert, N.S. Wingreen, and J.W. Shaevitz. Capillary interactions drive the self-organization of bacterial colonies. bioRxiv (2024)
- E. Han, C. Fei, R. Alert, K. Copenhagen, M.D. Koch, N.S. Wingreen, and J.W. Shaevitz. Local polar order controls mechanical stress and triggers layer formation in Myxococcus xanthus colonies. Nat. Commun. (2025)
- R. Alert, A. Martínez-Calvo, and S.S. Datta. Cellular Sensing Governs the Stability of Chemotactic Fronts. PRL (2022)
- T. Bhattacharjee*, D.B. Amchin*, R. Alert*, J.A. Ott, and S.S. Datta. Chemotactic smoothing of collective migration. eLife (2022)
- K. Copenhagen*, R. Alert*, N.S. Wingreen, and J.W. Shaevitz. Topological defects promote layer formation in Myxococcus xanthus colonies. Nat. Phys. (2021)
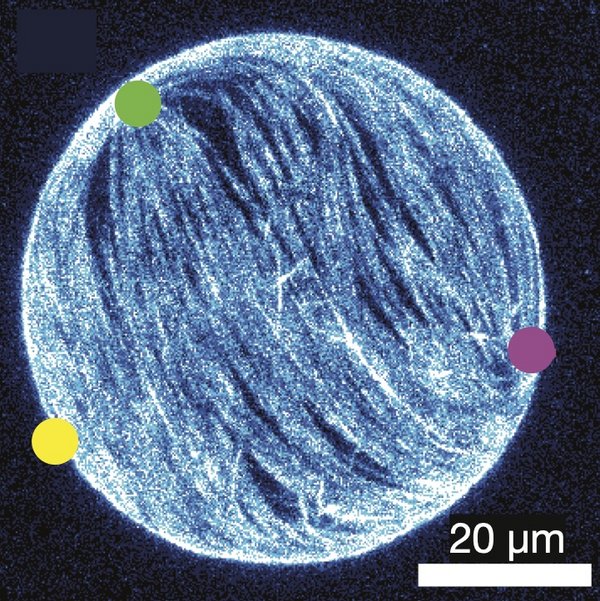
Image from F.C. Keber, E. Loiseau, T. Sanchez, S.J. DeCamp, L. Giomi, M.J. Bowick, M.C. Marchetti, Z. Dogic, and A.R. Bausch. Topology and dynamics of active nematic vesicles. Science 345, 1135 (2014)
Active droplets
Many biological and reconstituted systems behave as active droplets. Examples include biomolecular condensates, the mitotic spindle, cellular tissues, bacterial biofilms, and synthetic vesicles containing active nematic films. Because of their internal driving, active droplets often break symmetry and change shape spontaneously. To understand these phenomena, I study the morphological stability of active droplets.
Publications
R. Alert. Fingering instability of active nematic droplets. J. Phys. A (2022)
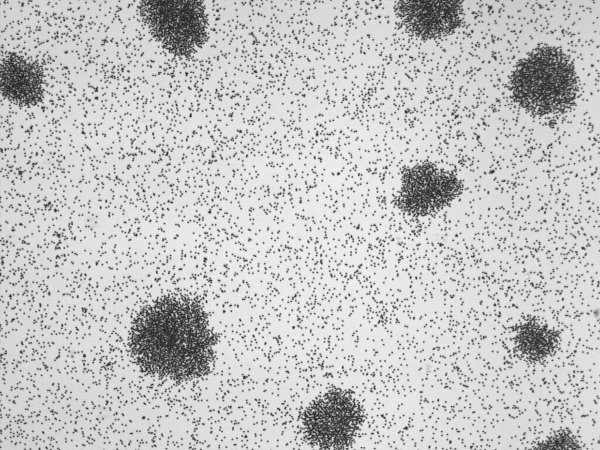
Image from J. Zhang*, R. Alert*, J. Yan, N.S. Wingreen, and S. Granick. Nat. Phys. (2021)
Phase transitions in active matter
We use active colloids as controlled model systems to study phase transitions in active matter. For example, self-propelled particles can condense even if they repel each other. This phase transition, known as motility-induced phase separation, has become a paradigmatic example of active-matter phenomena. Another landmark phase transition in active matter is the flocking transition, whereby active agents like birds align and move collectively. We study how interparticle torques enable new mechanisms for these phase transitions in self-propelled Janus colloids. Motivated by these systems, we also develop the statistical mechanics of systems with non-reciprocal interactions, which do not obey Newton's action-reaction law.
Publications
- Y. Shi, R. Moessner, R. Alert, and M. Bukov. General Hamiltonian description of nonreciprocal interactions. arXiv (2025)
- S. Das, M. Ciarchi, Z. Zhou, J. Yan, J. Zhang, and R. Alert. Flocking by Turning Away. PRX (2024)
- J. Zhang*, R. Alert*, J. Yan, N.S. Wingreen, and S. Granick. Active phase separation by turning towards regions of higher density. Nat. Phys. (2021)

Image from J. Yan, C. Fei, S. Mao, A. Moreau, N.S. Wingreen, A. Košmrlj, H.A. Stone, and B.L. Bassler. Mechanical instability and interfacial energy drive biofilm morphogenesis. eLife 8, e43920 (2019)
Mechanics of biofilm growth and morphogenesis
Biofilms are surface-adhered communities of bacterial cells embedded in a matrix of secreted polymers. As cells grow and proliferate, mechanical stress builds up in the biofilm. We have studied how the mechanics of biofilm growth governs biofilm morphogenesis. In particular, we have studied how wrinkle patterns emerge from the spatiotemporal dynamics of stress accumulation in growing biofilms. We also study the statistics of stress fluctuations in growing biofilms.
Publications
Q. Zhang, J. Li, J. Nijjer, H. Lu, M. Kothari, R. Alert, T. Cohen, and J. Yan. Morphogenesis and cell ordering in confined bacterial biofilms. PNAS (2021)
C. Fei, S. Mao, J. Yan, R. Alert, H.A. Stone, B.L. Bassler, N.S. Wingreen, and A. Košmrlj. Nonuniform growth and surface friction determine bacterial biofilm morphology on soft substrates. PNAS (2020)
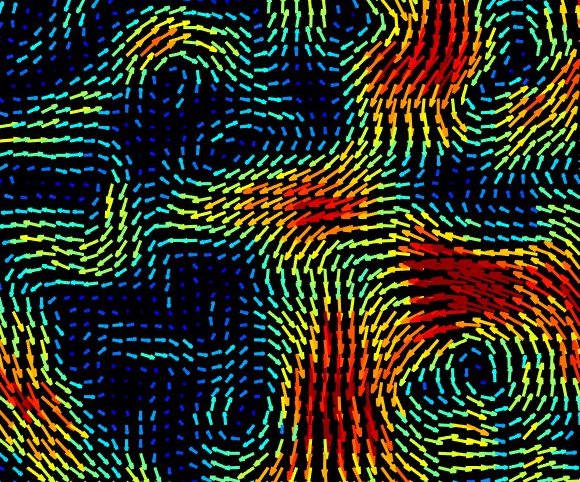
Image from B. Martínez-Prat*, R. Alert*, F. Meng, J. Ignés-Mullol, J-F. Joanny, J. Casademunt, R. Golestanian, and F. Sagués. PRX (2021)
Active turbulence
Active fluids are driven internally by their microscopic components, and hence they can flow spontaneously without applying external forces. Examples include suspensions of bacteria, cytoskeletal components, self-propelled particles, and even epithelial tissues. All these systems exhibit turbulent-like chaotic flows driven by activity. We study the statistical properties of active turbulence, trying to understand how they differ from those of classic inertial turbulence.
Publications
- M. Hillebrand and R. Alert. Discontinuous Transition to Active Nematic Turbulence. arXiv (2025)
- I. Lavi, R. Alert, J-F. Joanny, and J. Casademunt. Dynamical arrest in active nematic turbulence. arXiv (2024)
- I. Lavi, R. Alert, J-F. Joanny, and J. Casademunt. Nonlinear Spontaneous Flow Instability in Active Nematics. PRL (2025)
- R. Alert, J. Casademunt, and J-F. Joanny. Active Turbulence. Annu. Rev. Condens. Matter Phys. (2022)
- B. Martínez-Prat*, R. Alert*, F. Meng, J. Ignés-Mullol, J-F. Joanny, J. Casademunt, R. Golestanian, and F. Sagués. Scaling Regimes of Active Turbulence with External Dissipation. PRX (2021)
- R. Alert, J-F. Joanny, and J. Casademunt. Universal scaling of active nematic turbulence. Nat. Phys. (2020)
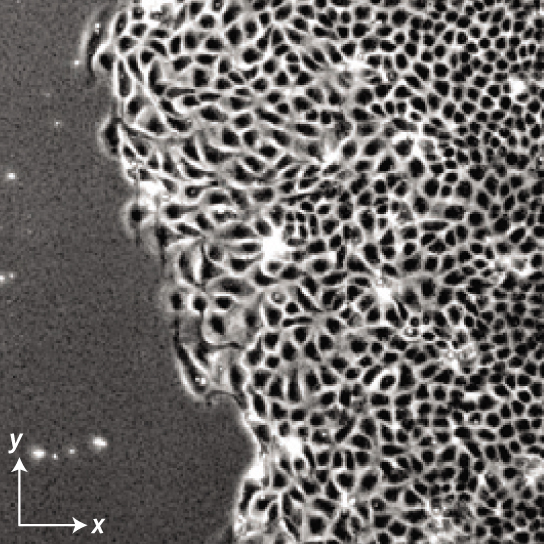
Image from X. Trepat, M.R. Wasserman, T.E. Angelini, E. Millet, D.A. Weitz, J.P. Butler, and J.J. Fredberg. Physical forces during collective cell migration. Nat. Phys. 5, 426 (2009)
Collective cell migration and tissue morphology
Collective cell migration is a key driver of embryonic development, wound healing, and some types of cancer invasion. I study how cells coordinate their motion, and how their collective migration impacts tissue morphology. For example, we propose active polar fluid models of tissue spreading, and we analyze experiments that measure the traction forces exerted by cells on a deformable substrate. Using this approach, we address collective mechanical phenomena in tissues, such as their wetting behavior, morphological instabilities, collective durotaxis, and structural transitions.
Publications
L. Rossetti, S. Grosser, J.F. Abenza, L. Valon, P. Roca-Cusachs, R. Alert, and X. Trepat. Optogenetic generation of leader cells reveals a force-velocity relation for collective cell migration. Nat. Phys. (2024)
T. Brandstätter*, D.B. Brückner*, Y.L. Han, R. Alert, M. Guo, and C.P. Broedersz. Curvature induces active velocity waves in rotating spherical tissues. Nat. Commun. (2023)
M-E. Pallarès*, I. Pi-Jaumà*, I.C. Fortunato, V. Grazu, M. Gómez-González, P. Roca-Cusachs, J.M. de la Fuente, R. Alert, R. Sunyer, J. Casademunt, and X. Trepat. Stiffness-dependent active wetting enables optimal collective cell durotaxis. Nat. Phys. (2023)
M.A Heinrich*, R. Alert*, A.E. Wolf*, A. Košmrlj, and D.J. Cohen. Self-assembly of tessellated tissue sheets by expansion and collision. Nat. Commun. (2022)
I. Pi-Jaumà, R. Alert, and J. Casademunt. Collective durotaxis of cohesive cell clusters on a stiffness gradient. EPJE (2022)
R. Alert and X. Trepat. Living Cells on the Move. Phys. Today (2021)
M.A Heinrich, R. Alert, J. LaChance, T.J. Zajdel, A. Košmrlj, and D.J. Cohen. Size-dependent patterns of cell proliferation and migration in freely-expanding epithelia. eLife (2020)
R. Alert and X. Trepat. Physical Models of Collective Cell Migration. Annu. Rev. Condens. Matter Phys. (2020)
R. Alert, C. Blanch-Mercader, and J. Casademunt. Active Fingering Instability in Tissue Spreading. PRL (2019)
R. Alert and J. Casademunt. Role of Substrate Stiffness in Tissue Spreading: Wetting Transition and Tissue Durotaxis. Langmuir (2019)
C. Pérez-González*, R. Alert*, C. Blanch-Mercader, M. Gómez-González, T. Kolodziej, E. Bazellières, J. Casademunt, and X. Trepat. Active wetting of epithelial tissues. Nat. Phys. (2019)
B. Smeets, R. Alert, J. Pešek, I. Pagonabarraga, H. Ramon, and R. Vincent. Emergent structures and dynamics of cell colonies by contact inhibition of locomotion. PNAS (2016)
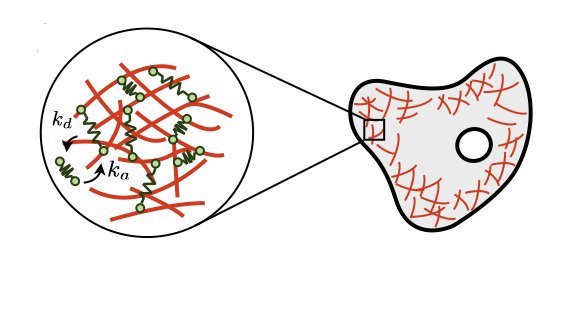
Image from D. Oriola*, R. Alert*, and J. Casademunt. PRL (2017)
Mechanics of active gels
Biological materials such as the actomyosin cytoskeleton, the mitotic spindle, and epithelial tissues are active gels, i.e. viscoelastic media driven internally by non-equilibrium molecular processes. I study how these molecular processes control the mechanical properties of active gels. In particular, we derived the hydrodynamic equations of active gels from the dynamics of their crosslinker proteins. This way, we unveiled how the breaking of detailed balance at the molecular scale gives rise to active stresses and tunes otherwise passive properties such as the gel's viscosity.
Publications
D. Oriola*, R. Alert*, and J. Casademunt. Fluidization and Active Thinning by Molecular Kinetics in Active Gels. PRL (2017)

Image from R. Alert, J. Casademunt, and P. Tierno. PRL (2014)
Phase transitions in colloidal crystals
Crystals made of colloidal particles can be imaged with single-particle resolution, and interparticle interactions can be externally tuned. Leveraging these features, I use colloidal crystals as an experimental model system to study fundamental aspects of phase transitions. We combine theory, simulations, and experiments to study the structural transitions of a two-dimensional magnetic colloidal crystal assembled on a micropatterned substrate. The interplay between the pinning imposed by the substrate and the intrinsic anisotropy of the magnetic dipolar interactions gives rise to a new type of phase transition with unprecedented equilibrium and kinetic properties. This new transition has properties in between those of first- and second-order transitions.
Publications
R. Alert, P. Tierno, and J. Casademunt. Mixed-order phase transition in a colloidal crystal. PNAS (2017)
R. Alert, P. Tierno, and J. Casademunt. Formation of metastable phases by spinodal decomposition. Nat. Commun. (2016)
R. Alert, J. Casademunt, and P. Tierno. Landscape-Inversion Phase Transition in Dipolar Colloids: Tuning the Structure and Dynamics of 2D Crystals. PRL (2014)
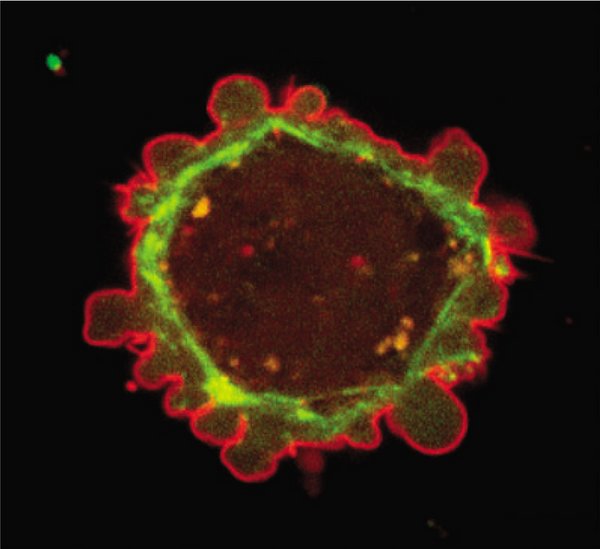
Image from G.T. Charras. A short history of blebbing. J. Microsc. 231, 466 (2008)
Membrane-cortex adhesion and bleb nucleation
The cell membrane (red) is attached to the underlying actin cortex (green) by specific linker proteins. We proposed a mechanochemical model for membrane-cortex adhesion that couples the binding kinetics of the linker proteins to membrane deformations and cortical tension. With this model, we predicted the conditions for membrane detachment, and we interpreted micropipette aspiration experiments. We also study the effect of membrane-cortex adhesion on membrane fluctuations, providing predictions for fluctuation spectroscopy experiments.
A local detachment of the membrane leads to blister-like protrusions called blebs. We studied bleb nucleation, i.e. the spontaneous formation of blebs, which we predict to be governed by a rupture process called membrane peeling. We quantified the kinetics of bleb nucleation by means of stochastic simulations.
Publications
R. Alert and J. Casademunt. Bleb Nucleation through Membrane Peeling. PRL (2016)
R. Alert, J. Casademunt, J. Brugués, and P. Sens. Model for Probing Membrane-Cortex Adhesion by Micropipette Aspiration and Fluctuation Spectroscopy. Biophys. J. (2015)