
Research
The main research topic in our group Self-Organization of Multicellular Systems is the biophysics of cells and tissues (nomen est omen), but we have wider research interests in mathematical biology and soft matter physics.
Biological Physics of Cells and Tissues
Our main research focus is the mechanics of cells and tissues. In particular, we want to understand how the mechanical behaviour of tissues emerges from the mechanics at the cell scale, and how robust development is compatible with mechanical constraints and biological variability. We therefore derive novel continuum theories for biological tissues and apply them to experimental data of the rich mechanical behaviour of tissues during development. Although our research is theoretical, we work in close collaboration with experimental groups at the MPI-CBG and beyond.
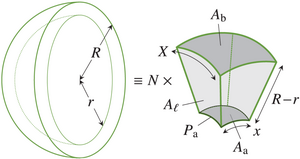
Geometry of T1 transitions in epithelia
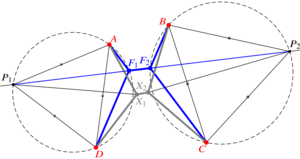
The flows of tissues of epithelial cells often involve T1 transitions. These neighbour exchanges are irreversible rearrangements crossing an energy barrier. Here, by an exact geometric construction, I determine this energy barrier for general, isolated T1 transitions dominated by line tensions. I show how deviations from regular cell packing reduce this energy barrier, but find that line tension fluctuations increase it on average. By another exact construction, I show how nonlinear tensions in vertex models of epithelial tissues also resist T1 transitions. My results thus form the basis for coarse-grained descriptions of cell neighbour exchanges in continuum models of epithelia. [Text and figure from Haas, arXiv (2025)]
Euler buckling on curved surfaces
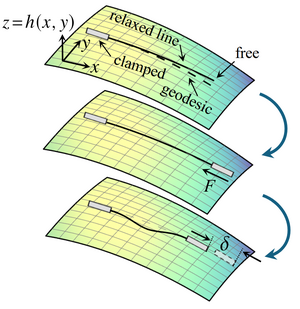
Euler buckling epitomises mechanical instabilities: An inextensible straight elastic line buckles under compression when the compressive force reaches a critical value F*> 0. Here, we extend this classical, planar instability to the buckling under compression of an inextensible relaxed elastic line on a curved surface. By weakly nonlinear analysis of an asymptotically short elastic line, we reveal that the buckling bifurcation changes fundamentally: The critical force for the lowest buckling mode is F* = 0 and higher buckling modes disconnect from the undeformed branch to connect in pairs. Solving the buckling problem numerically, we additionally find a new post-buckling instability: A long elastic line on a curved surface snaps through under sufficient compression. Our results thus set the foundations for understanding the buckling instabilities on curved surfaces that pervade the emergence of shape in biology. [Text and figure from Zhao and Haas, arXiv (2025)]
A model for boundary-driven tissue morphogenesis
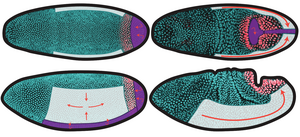
Tissue deformations during morphogenesis can be active, driven by internal processes, or passive, resulting from stresses applied at their boundaries. Here, we introduce the Drosophila hindgut primordium as a model for studying boundary-driven tissue morphogenesis. We characterize its deformations and show that its complex shape changes can be a passive consequence of the deformations of the active regions of the embryo that surround it. First, we find an intermediate characteristic triangular shape in the 3D deformations of the hindgut. We construct a minimal model of the hindgut primordium as an elastic ring deformed by active midgut invagination and germ band extension on an ellipsoidal surface, which robustly captures the symmetry-breaking into this triangular shape. We then quantify the 3D kinematics of the tissue by a set of contours and discover that the hindgut deforms in two stages: an initial translation on the curved embryo surface followed by a rapid breaking of shape symmetry. We extend our model to show that the contour kinematics in both stages are consistent with our passive picture. Our results suggest that the role of in-plane deformations during hindgut morphogenesis is to translate the tissue to a region with anisotropic embryonic curvature and show that uniform boundary conditions are sufficient to generate the observed nonuniform shape change. Our work thus provides a possible explanation for the various characteristic shapes of blastopore-equivalents in different organisms and a framework for the mechanical emergence of global morphologies in complex developmental systems. [Text and figure from Alber, Zhao, et al., arXiv (2025)]
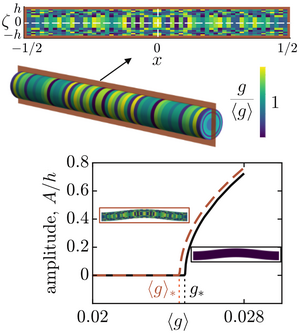
(Un)buckling mechanics of epithelial monolayers under compression
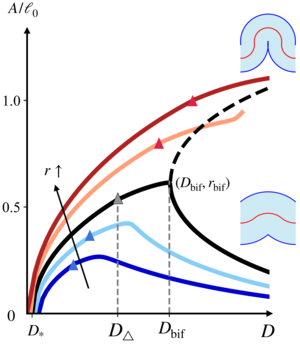
When cell sheets fold during development, their apical or basal surfaces constrict and cell shapes approach the geometric singularity in which these surfaces vanish. Here, we reveal the mechanical consequences of this geometric singularity for tissue folding in a minimal vertex model of an epithelial monolayer. In simulations of the buckling of the epithelium under compression and numerical solutions of the corresponding continuum model, we discover an "unbuckling" bifurcation: At large compression, the buckling amplitude can decrease with increasing compression. By asymptotic solution of the continuum equations, we reveal that this bifurcation comes with a large stiffening of the epithelium. Our results thus provide the mechanical basis for absorption of compressive stresses by tissue folds such as the cephalic furrow during germband extension in Drosophila. [Text and figure from Guha Ray and Haas, arXiv (2024)]
Mechanics of poking a cyst
Indentation tests are classical tools to determine material properties. For biological samples such as cysts of cells, however, the observed force-displacement relation cannot be expected to follow predictions for simple materials. Here, by solving the Pogorelov problem of a point force indenting an elastic shell for a purely nonlinear material, we discover that complex material behaviour can even give rise to new scaling exponents in this force-displacement relation. In finite-element simulations, we show that these exponents are surprisingly robust, persisting even for thick shells indented with a sphere. By scaling arguments, we generalise our results to pressurised and pre-stressed shells, uncovering additional new scaling exponents. We find these predicted scaling exponents in the force-displacement relation observed in cyst indentation experiments. Our results thus form the basis for inferring the mechanisms that set the mechanical properties of these biological materials. [Text and figure from Zhao and Haas, arXiv (2024)]
Buckling by disordered growth
Buckling instabilities driven by tissue growth underpin key developmental events such as the folding of the brain. Tissue growth is disordered due to cell-to-cell variability, but the effects of this variability on buckling are unknown. Here, we analyse what is perhaps the simplest setup of this problem: the buckling of an elastic rod with fixed ends driven by spatially varying growth. Combining analytical calculations for simple growth fields and numerical sampling of random growth fields, we show that variability can increase as well as decrease the growth threshold for buckling, even when growth variability does not cause any residual stresses. For random growth, we find that the shift of the buckling threshold correlates with spatial moments of the growth field. Our results imply that biological systems can either trigger or avoid buckling by exploiting the spatial arrangement of growth variability. [Text and figure from Ramachandran et al., arXiv (2024)]
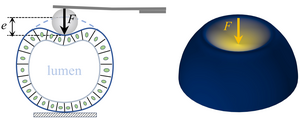
Shaping epithelial lumina under pressure
The formation of fluid- or gas-filled lumina surrounded by epithelial cells pervades development and disease. While reviewing the balance between lumen pressure and mechanical forces from the surrounding cells that governs lumen formation, we develop simple mean-field models that describe the mechanical side of this balance that emerges from the mechanical of the cells surrounding the lumen. We discuss how recent work is beginning to elucidate how nonlinear and active mechanics and anisotropic biomechanical structures must conspire to overcome the isotropy of pressure to form complex, non-spherical lumina, and show in particular how mechanical nonlinearities can break the symmetry of a spherical cyst in a mean-field vertex model. [Text and figure from Haas & Bovyn, Biochem. Soc. Trans. 52, 331 (2024)]
Hepatoblast iterative apicobasal polarization is regulated by extracellular matrix remodeling

Hepatocytes have a unique multiaxial polarity with several apical and basal surfaces. The prevailing model for the emergence of this multipolarity and the coordination of lumen formation between adjacent hepatocytes is based on asymmetric cell division. Here, investigating polarity generation in liver cell progenitors, the hepatoblasts, during liver development in vivo and in vitro, we found that this model cannot explain the observed dynamics of apical lumen formation in the embryonic liver. Instead, we identified a new mechanism of multi-axial polarization: We found that polarization can be initiated in a cell-autonomous manner by re-positioning apical recycling endosomes (AREs) to the cell cortex via fibronectin sensing through Integrin αV. Using live cell imaging we showed that this process repeats, leading to multiaxial polarity independently of cell division. We found that the establishment of oriented trafficking leads to the secretion of the metalloprotease MMP13, allowing neighboring hepatoblasts to synchronize their polarization by sensing extracellular matrix (ECM) distribution and enabling lumen opening. Finally, active remodeling of ECM in the proximity of nascent apical surfaces closes a positive feedback loop of polarization, whereas disruption of this loop by either blocking MMP13 or downregulating Integrin αV prevents the formation of the bile canaliculi network. Integration of this feedback loop into a simple mathematical model reproduces the observed dynamics of bile canaliculi network formation during liver development quantitatively. Our combined findings thus suggest a new mechanism of polarization coupling to self-organization at the tissue scale. [Text and figure from Delpierre et al., biorXiv (2024)]
Cut it out: Out-of-plane stresses in cell sheet folding of Volvox embryos

The folding of cellular monolayers pervades embryonic development and disease. It results from stresses out of the plane of the tissue, often caused by cell shape changes including cell wedging via apical constriction. These local cellular changes need not however be compatible with the global shape of the tissue. Such geometric incompatibilities lead to residual stresses that have out-of-plane components in curved tissues, but the mechanics and function of these out-of-plane stresses are poorly understood, perhaps because their quantification has proved challenging. Here, we overcome this difficulty by combining laser ablation experiments and a mechanical model to reveal that such out-of-plane residual stresses exist and also persist during the inversion of the spherical embryos of the green alga Volvox. We show how to quantify the mechanical properties of the curved tissue from its unfurling on ablation, and reproduce the tissue shape sequence at different developmental timepoints quantitatively by our mechanical model. Strikingly, this reveals not only clear mechanical signatures of out-of-plane stresses associated with cell shape changes away from those regions where cell wedging bends the tissue, but also indicates an adaptive response of the tissue to these stresses. Our results thus suggest that cell sheet folding is guided mechanically not only by cell wedging, but also by out-of-plane stresses from these additional cell shape changes. [Text and figure from Haas & Höhn, biorXiv (2023)]
A multi-tiered mechanical mechanism shapes the early neural plate
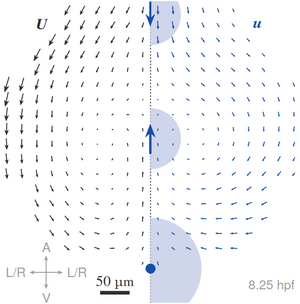
The formation of complex tissues during embryonic development requires an intricate spatiotemporal coordination of local mechanical processes regulating global tissue morphogenesis. Here, we uncover a novel mechanism that mechanically regulates the shape of the anterior neural plate (ANP), a vital forebrain precursor, during zebrafish gastrulation. Combining in vivo and in silico approaches we reveal that the ANP is shaped by global tissue flows regulated by distinct force generating processes. We show that mesendoderm migration and E-cadherin-dependent differential tissue interactions control distinct flow regimes in the neuroectoderm. Initial opposing flows lead to progressive tissue folding and neuroectoderm internalisation which in turn provide forces driving ANP tissue reshaping. We find that convergent extension is dispensable for internalisation but required for ANP tissue extension. Our results highlight how spatiotemporal regulation and coupling of different mechanical processes between tissues in the embryo controls the first folding event in the developing brain. [Text and figure from Inman et al., biorXiv (2023)]
Hepatocyte apical bulkheads provide a mechanical means to oppose bile pressure
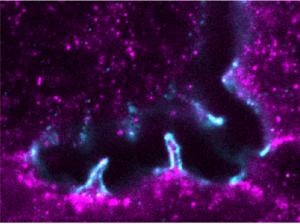
In the liver, hepatocyte cells grow their apical surfaces anisotropically to generate a 3D network of bile canaliculi (BC). BC elongation is ensured by apical bulkheads, membrane extensions that traverse the lumen and connect juxtaposed hepatocytes. We hypothesize that apical bulkheads are mechanical elements that shape the BC lumen in liver development but also counteract elevated biliary pressure. Here, by resolving their structure using STED microscopy, we found that they are sealed by tight junction loops, connected by adherens junctions, and contain contractile actomyosin, characteristics of mechanical function. Apical bulkheads persist at high pressure upon microinjection of fluid into the BC lumen, and laser ablation demonstrated that they are under tension. A mechanical model based on ablation results revealed that apical bulkheads double the pressure BC can hold. Apical bulkhead frequency anticorrelates with BC connectivity during mouse liver development, consistent with predicted changes in biliary pressure. Our findings demonstrate that apical bulkheads are load-bearing mechanical elements that could protect the BC network against elevated pressure. [Text and figure from Bebelman, Bovyn, et al., J. Cell Biol. 222, e202208002 (2023)]
Morphoelasticity of large bending deformations of cell sheets during development
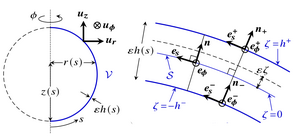
Deformations of cell sheets during morphogenesis are driven by developmental processes such as cell division and cell shape changes. In morphoelastic shell theories of development, these processes appear as variations of the intrinsic geometry of a thin elastic shell. However, morphogenesis often involves large bending deformations that are outside the formal range of validity of these shell theories. By asymptotic expansion of three-dimensional incompressible morphoelasticity in the limit of a thin shell, we have derived a shell theory for large intrinsic bending deformations and emphasize the resulting geometric material anisotropy and the elastic role of cell constriction. Taking the invagination of the green alga Volvox as a model developmental event, we have shown how results for this theory differ from those for a classical shell theory that is not formally valid for these large bending deformations and reveal how these geometric effects stabilize invagination. [Text and figure from Haas & Goldstein, Phys. Rev. E 103, 022411 (2021).]
Nonlinear and nonlocal elasticity in coarse-grained differential-tension models of epithelia
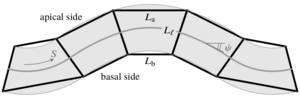
The shapes of epithelial tissues result from a complex interplay of contractile forces in the cytoskeleta of the cells in the tissue and adhesion forces between them. A host of discrete, cell-based models describe these forces by assigning different surface tensions to the apical, basal, and lateral sides of the cells. These differential-tension models have been used to describe the deformations of epithelia in different living systems, but the underlying continuum mechanics at the scale of the epithelium are still unclear. We have derived a continuum theory for a simple differential-tension model of a two-dimensional epithelial monolayer and study the buckling of this epithelium under imposed compression. The analysis reveals how the cell-level properties encoded in the differential-tension model lead to linear and nonlinear elastic as well as nonlocal, nonelastic behavior at the continuum level. [Text and figure from Haas & Goldstein, Phys. Rev. E 99, 022411 (2019).]
Embryonic inversion in Volvox carteri: The flipping and peeling of elastic lips
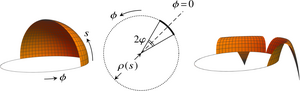
The embryos of the green alga Volvox carteri are spherical sheets of cells that turn themselves inside out at the close of their development through a program of cell shape changes. This process of inversion is a model for morphogenetic cell sheet deformations; it starts with four lips opening up at the anterior pole of the cell sheet, flipping over, and peeling back to invert the embryo. Experimental studies have revealed that inversion is arrested if some of these cell shape changes are inhibited, but the mechanical basis for these observations has remained unclear. We have analyzed the mechanics of this inversion by deriving an averaged elastic theory for these lips and we have interpreted the experimental observations in terms of the mechanics and evolution of inversion. [Text and figure from Haas & Goldstein, Phys. Rev. E 98, 052415 (2018).]
The noisy basis of morphogenesis
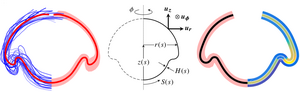
Variability is emerging as an integral part of development. It is therefore imperative to ask how to access the information contained in this variability. Yet most studies of development average their observations and, discarding the variability, seek to derive models, biological or physical, that explain these average observations. We have analysed this variability in a study of cell sheet folding in the green alga Volvox, whose spherical embryos turn themselves inside out in a process sharing invagination, expansion, involution, and peeling of a cell sheet with animal models of morphogenesis. We have generalised our earlier, qualitative model of the initial stages of inversion by combining ideas from morphoelasticity and shell theory. Together with three-dimensional visualisations of inversion using light sheet microscopy, we have obtained a detailed, quantitative model of the entire inversion process. With this model, we have shown how the variability of inversion reveals that two separate, temporally uncoupled processes drive the initial invagination and subsequent expansion of the cell sheet. This implies a prototypical transition towards higher developmental complexity in the volvocine algae and provides proof of principle of analysing morphogenesis based on its variability. [Figure and text from Haas et al., PLoS Biol. 16, e2005536 (2018).]
Dynamics and Mechanics of a Volvox embryo turning itself inside out
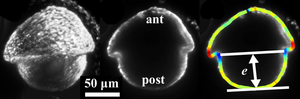
Deformations of cell sheets are ubiquitous in early animal development, often arising from a complex and poorly understood interplay of cell shape changes, division, and migration. We have explored perhaps the simplest example of cell sheet folding: the “inversion” process of the algal genus Volvox, during which spherical embryos turn themselves inside out through a process hypothesized to arise from cell shape changes alone. We have used light sheet microscopy to obtain the first three-dimensional visualizations of inversion in vivo, and have developed the first theory of this process, in which cell shape changes appear as local variations of intrinsic curvature, contraction and stretching of an elastic shell. Our results support a scenario in which these active processes function in a defined spatiotemporal manner to enable inversion.
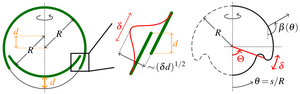
In later work, we have analysed the mechanics of the initial invagination, reminiscent of similar events during the development of higher organisms. Through a combination of asymptotic analysis and numerical studies of the bifurcation behaviour, we have illustrated how appropriate local deformations (i.e. cell shape changes represented as changes of the intrinsic geometry of the cell sheet) can overcome global constraints to initiate inversion.
[Text and figures from Höhn et al., Phys. Rev. Lett. 114, 178101 (2015) and Haas and Goldstein, J. R. Soc. Interface 12, 20150671 (2015).]
Other Research Interests
Impossible ecologies: Interaction networks and stability of coexistence in ecological communities
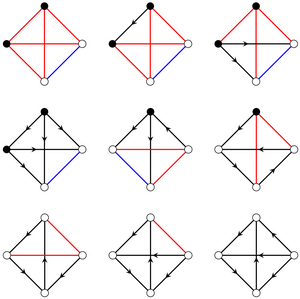
Does an ecological community allow stable coexistence? Identifying the general principles that determine the answer to this question is a central problem of theoretical ecology. Random matrix theory approaches have uncovered the general trends of the effect of competitive, mutualistic, and predator-prey interactions between species on stability of coexistence. However, an ecological community is determined not only by the counts of these different interaction types, but also by their network arrangement. This cannot be accounted for in a direct statistical description that would enable random matrix theory approaches. Here, we therefore develop a different approach, of exhaustive analysis of small ecological communities, to show that this arrangement of interactions can influence stability of coexistence more than these general trends. We analyse all interaction networks of N⩽5 species with Lotka-Volterra dynamics by combining exact results for N⩽3 species and numerical exploration. Surprisingly, we find that a very small subset of these networks are "impossible ecologies", in which stable coexistence is non-trivially impossible. We prove that the possibility of stable coexistence in general ecologies is determined by similarly rare "irreducible ecologies". By random sampling of interaction strengths, we then show that the probability of stable coexistence varies over many orders of magnitude even in ecologies that differ only in the network arrangement of identical ecological interactions. Finally, we demonstrate that our approach can reveal the effect of evolutionary or environmental perturbations of the interaction network. Overall, this work reveals the importance of the full structure of the network of interactions for stability of coexistence in ecological communities. [Text and figure from Meng et al., arXiv (2023).]
Stabilisation of Microbial Communities by Responsive Phenotypic Switching
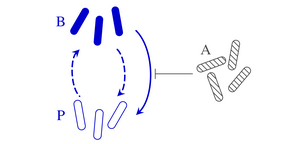
Clonal microbes can switch between different phenotypes and recent theoretical work has shown that stochastic switching between these subpopulations can stabilize microbial communities. This phenotypic switching need not be stochastic, however, but can also be in response to environmental factors, both biotic and abiotic. Motivated by the bacterial persistence phenotype, we have explored the ecological effects of such responsive switching by analyzing phenotypic switching in response to competing species. We have shown how the stability of microbial communities with responsive switching differs generically from that of communities with stochastic switching only. To understand this effect, we have gone on to analyse simple two-species models. Combining exact results and numerical simulations, we have extended the classical stability results for models of two competing species without phenotypic variation to the case where one of the two species switches, stochastically and responsively, between two phenotypes. In particular, we have shown that responsive switching can stabilize coexistence even when stochastic switching on its own does not affect the stability of the community. [Text and figure from Haas et al., Phys. Rev. Research 4, 033224 (2022).]
Turing's diffusive threshold in random reaction-diffusion systems
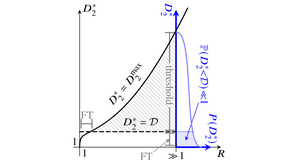
Turing instabilities of reaction-diffusion systems can only arise if the diffusivities of the chemical species are sufficiently different. This threshold is unphysical in most systems with N=2 diffusing species, forcing experimental realizations of the instability to rely on fluctuations or additional nondiffusing species. We have asked whether this diffusive threshold lowers for N>2 to allow "true" Turing instabilities. Inspired by May's analysis of the stability of random ecological communities, we have analyzed the probability distribution of the diffusive threshold in reaction-diffusion systems defined by random matrices describing linearized dynamics near a homogeneous fixed point. In the numerically tractable cases N<7, we have found that the diffusive threshold becomes more likely to be smaller and physical as N increases and that most of these many-species instabilities cannot be described by reduced models with fewer species. [Text and figure from Haas & Goldstein, Phys. Rev. Lett. 126, 238101 (2021).]
Subpopulations and stability in microbial communities
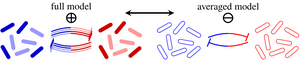
In microbial communities, each species often has multiple, distinct phenotypes, but studies of ecological stability have largely ignored this subpopulation structure. We have shown that such implicit averaging over phenotypes leads to incorrect linear stability results. We have gone on to analyze the effect of phenotypic switching in detail in an asymptotic limit and have partly overturned classical stability paradigms: Abundant phenotypic variation is linearly destabilizing but, surprisingly, a rare phenotype such as bacterial persisters has a stabilizing effect. We have extended these results by showing how phenotypic variation modifies the stability of the system to large perturbations such as antibiotic treatments. [Text and figure from Haas et al., Phys. Rev. Research 2, 022036(R) (2020).]
Shape-shifting polygonal and polyhedral droplets
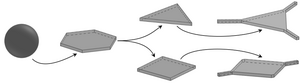
Cooled oil emulsion droplets in aqueous surfactant solution have been observed to flatten into a remarkable host of polygonal shapes with straight edges and sharp corners, but different driving mechanisms—(i) a partial phase transition of the liquid bulk oil into a plastic rotator phase near the droplet interface and (ii) buckling of the interfacially frozen surfactant monolayer enabled by a drastic lowering of surface tension—have been proposed. We have explored the simplest geometric competition between this phase transition and surface tension in planar polygons to recover the observed sequence of shapes and their statistics in qualitative agreement with experiments, and to explain the formation of protrusions sprouting from the droplet vertices and the puncturing of planar polygonal droplets.

In later work, combining experiment and theory, we have analyzed the initial stages of the evolution of these “shape-shifting” droplets, during which a polyhedral droplet flattens into a polygonal platelet under cooling and gravity. Using reflected-light microscopy, we have revealed how icosahedral droplets evolve through an intermediate octahedral stage to flatten into hexagonal platelets. This behavior is reproduced by a theoretical model of the phase transition mechanism, but the buckling mechanism can only reproduce the flattening if the deformations are driven by buoyancy. This requires surface tension to decrease by several orders of magnitude during cooling and yields bending modulus estimates orders of magnitude below experimental values.
Others have since shown that the observed phenomena are also consistent with an "augmented" elastic mechanism based on the intrinsic curvature of the droplet surface, but we have commented that this interplay between surface tension and intrinsic curvature is in fact mathematically equivalent to the physically very different phase-transition mechanism. The mathematical models cannot therefore distinguish between the two mechanisms, and we have argued that differences in experimental suggest that the observed phenomena are therefore physically very different realizations of a general "shape-shifting" mechanism based on the inter-play of positive surface tension and negative edge tension in faceted droplets. [Text and figures from Haas et al., Phys. Rev. Lett. 118, 088001 (2017), iid., Phys. Rev. Research 1, 023017 (2019), and iid., Phys. Rev. Lett. 126, 259801 (2021).]
Biophysical Models of RNA secondary structure prediction
Most of the many computational methods that have been developed for the prediction of RNA secondary structure and the prediction of the consensus structure from an alignment of sequences ignore the biophysical factors - including kinetic and co-transcriptional effects during RNA folding - that affect this secondary structure. In the framework of stochastic context-free grammars, we have developed an iterative algorithm, punningly named "Oxfold", that combines a simple model of the kinetics of RNA folding with an evolutionary model. By showing that the model outperforms previous non-kinetic grammatical models and compares favourably to thermodynamic models that do not model folding kinetics, we have established the importance of these kinetic effects for RNA secondary structure.