Research

The Anderson insulator is a quantum state of matter which does not conduct. This is due to disorder induced destructive interference of the electron wave function; a manifestly non-interacting, single-particle phenomena. What is the fate of this insulating state when the constituent particles interact among themselves? Will it become conducting or will it remain an ideal insulator? If the latter, what are the properties of the resulting insulating state? These are the central questions posed in the field of many-body localization, with the possible insulating phase being many-body localized.

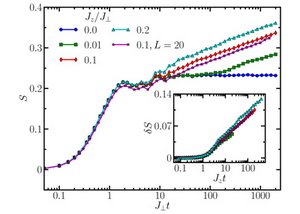
In our work, we have explored the entanglement properties in the many-body localized phase. Preparing the system in a generic non-entangled state, the quantum dynamics are found to generate entanglement that grows logarithmically in time, with a saturation value that follows a volume law. This should be contrasted with the non-interacting Anderson insulator, where the entanglement is local and non-extensive in the same setup. At the same time, particle transport does not take place. The Anderson insulator and the many-body localized phase are thus fundamentally different insulating states.

For further reading see:

Jens H. Bardarson, Frank Pollmann, Joel E. Moore, Phys. Rev. Lett. 109, 017202 (2012)

Disorder, when strong enough, generally localizes all electrons. An exception is electrons at the surfaces of topological insulators, which due to their nontrivial topological properties manage to avoid localization. This property can, in fact, be used as a definition of a topological insulators.

We were at the forefront of demonstrating this for the case a 2D Dirac fermions, as realized on the surface of 3D topological insulators. In particular, we have shown that disorder always drives the surface of a strong topological insulator metallic -- sometimes referred to as supermetal. A strong topological insulator has an odd number of Dirac fermions in its surface; a weak topological insulator, in contrast, has an even number. Surprisingly, as we have shown, the weak topological insulator also avoids localization under rather general conditions.

In order to demonstrate these and other transport phenomena of Dirac fermions, we have developed a numerical technique based on the transfer matrix formalism in momentum space. This was needed to avoid the fermion doubling theorem, which states that an odd number of Dirac fermions can not be realized on a lattice in two dimensions.


For further reading see:

• Jens H. Bardarson, Joel E. Moore, Rep. Prog. Phys. 76, 056501 (2013).
• E. Rossi, J. H. Bardarson, M. S. Fuhrer, S. Das Sarma, Phys. Rev. Lett. 109, 096801 (2012).
• Roger S. K. Mong, Jens H. Bardarson, Joel E. Moore Phys. Rev. Lett. 108, 076804 (2012).
• J. H. Bardarson, M. V. Medvedyeva, J. Tworzydlo, A. R. Akhmerov, C. W. J. Beenakker, Phys. Rev. B 81, 121414(R) (2010).
• J. H. Bardarson, J. Tworzydlo, P. W. Brouwer, C. W. J. Beenakker, Phys. Rev. Lett. 99, 106801 (2007)

Topological insulators are bulk insulators with a metallic surface which can be described, in the simplest case, by a single Dirac fermion. What are the properties of this metallic state when the surface is curved, such as in a cylindrical wire? How are these properties revealed in experiments, in particular in quantum transport? Are there phenomena unique to this system?

The metallic surface of a topological insulator nanowire turns out to be gapped. This is an effect of the Dirac fermion's non-trivial Berry phase as it winds around the cylindrical surface. A magnetic flux along the length of the wire can cancel this Berry phase and close the gap, thereby giving rise to the presence of a perfectly transmitted mode. This leads to various characteristic transport phenomena in these wires, such as magneto-conductance oscillations with period h/e, and a distinct peak in the supercurrent in a Josephson junction setup.


For further reading see:

• Roni Ilan, Jens H. Bardarson, H. -S. Sim, Joel E. Moore, arXiv:1305.2210v1.
• Jens H. Bardarson, Joel E. Moore, Rep. Prog. Phys. 76, 056501 (2013).
• J. H. Bardarson, P. W. Brouwer, J. E. Moore, Phys. Rev. Lett. 105, 156803 (2010).
• J. H. Bardarson, J. Phys. A: Math. Theor. 41, 405203, (2008).
• J. H. Bardarson, J. Tworzydlo, P. W. Brouwer, C. W. J. Beenakker, Phys. Rev. Lett. 99, 106801 (2007)