Research
Statistical physics of active agents
Dynamics of biological and synthetic microswimmers
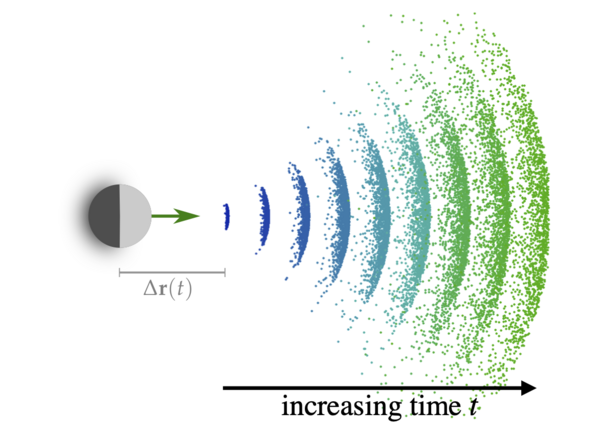
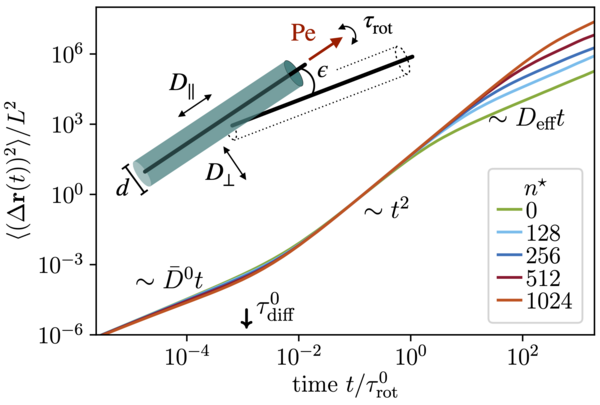
Microorganisms exhibit a large variety of swimming mechanisms to efficiently explore their environment. Whether bacteria, algae or synthetic swimmers, these microswimmers are out-of-equilibrium and extract energy from their environment to achieve biological functions. Quantifying their dynamics at the single-particle level is key to understanding how they behave in complex surroundings. Their spatiotemporal behavior is encoded in the intermediate scattering function, which constitutes the Fourier transform of the probability density of the particle's displacements. In particular, we have worked on characterizing the dynamical behavior of catalytic Janus colloids using exact solutions for the paradigmatic active Brownian particle model (right, lower panel) and the run-and-tumble behavior of E. coli bacteria in terms of renewal processes. We compare our theoretical predictions to observations of these synthetic and biological micro-swimmers measured by our experimental collaborators.
Relevant publications
New J. Phys. 26, 073041 (2024)
Phys. Rev. Lett. 132, 038302 (2024)
Phys. Rev. E 109, 014612 (2024)
Phys. Rev. Lett.121 (2018)
Soft Matter13 (2017)
Sci. Rep.6 (2016)
Press coverage
Newsroom Universität Innsbruck Einfaches Modell für komplexes Phänomen
Physics MagazineCharacterizing the Swimming Gait of a Bacterium
Newsroom Universität InnsbruckBakterien in Bewegung
First-passage-time statistics of active agents
Measuring first-passage-time (FPT) statistics allows quantifying the efficiency of a variety processes. We study the FPT properties of active Brownian particles to reach an absorbing wall in two dimensions. Employing a perturbation approach we obtain exact analytical predictions for the survival and FPT distributions for small Péclet numbers, measuring the importance of self-propulsion relative to diffusion. While randomly oriented active agents reach the wall faster than their passive counterpart, their initial orientation plays a crucial role in the FPT statistics. Using the median as a metric, we quantify this anisotropy and find that it becomes more pronounced at distances where persistent active motion starts to dominate diffusion.
Introducing a resetting mechanism, taking the particle back to a predefined position and orientation, reveals a mean FPT that becomes optimal at an intermediate resetting rate. The optimal resetting rate depends non-trivially on the initial distance to the boundary due to the intricate interplay of resetting, rotational Brownian noise, and active motion.
Relevant publications
Soft Matter (2025)
Phys. Rev. E 111 (2025)
Active transport in porous media
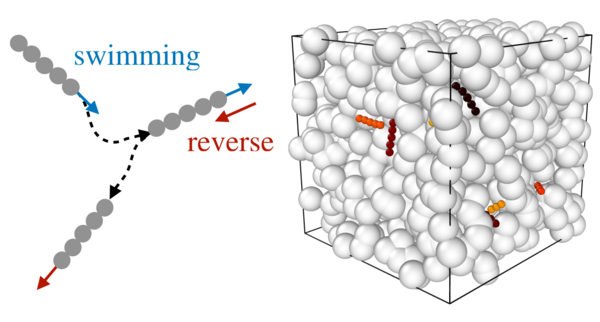
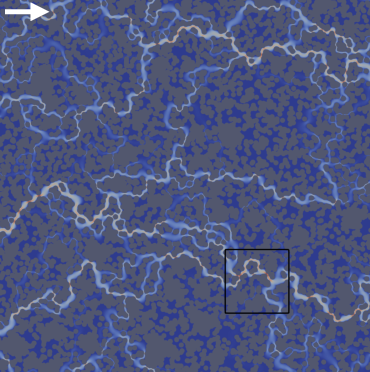
Efficient navigation through disordered, porous environments poses a major challenge for microorganisms and future synthetic cargo-carriers, which hold great potential for novel biomedical and environmental applications. In our work, we model the motion of active agents by self-propelled stiff polymers that employ a run-reverse mechanism at random times. Our findings show that spreading of active agents in porous media can be optimized by tuning their run lengths. We propose a geometric criterion and demonstrate that the optimal spreading occurs when the run lengths are comparable to the longest available pore length of the porous medium. These reversal mechanisms should be included in the strategies for microrobots to traverse porous environments and are relevant for efficient drug-delivery systems and bioremediation tools.
Relevant publication
Press coverage
Princeton press Researchers find the best way for bacteria to navigate maze-like environments
HHU Düsseldorf press Wie Bakterien aus Labyrinthen herausfinden
Entangled active matter
Crowding-enhanced diffusion of stiff active filaments
`Crowded is slower’ is a well studied problem in many fields ranging from caging in colloidal glasses to the evacuation of crowds to traffic jams. In striking contrast to these observations, we reveal that the diffusivity of self-propelled anisotropic agents, such as biofilaments and elongated bacteria, can be enhanced by orders of magnitude due to crowding. This counterintuitive `crowded is faster’ behavior is corroborated by a scaling theory based on the concept of a confining tube pioneered by Doi and Edwards. Our findings propose a novel way to control the mobility of individual self-propelled anisotropic agents in disordered environments by tuning the degree of crowding.
Relevant publication
Phys. Rev. Lett.125 (2020)
Press coverage
Physics Magazine Filaments Move Quickly Through a Crowd
Elastic properties of an entangled, active polymer solution
Furthermore, we study the viscoelastic properties of highly entangled, flexible, self-propelled polymers using Brownian dynamics simulations. Our results show that the active motion of the polymer increases the height of the stress plateau by orders of magnitude due to the emergence of grip forces at entanglement points. Identifying the activity-induced energy of a single polymer and the ratio of polymer length to self-propulsion velocity as relevant energy and time scales, we find the stress autocorrelation functions collapse across Péclet numbers. We predict that the long-time viscosity scales with polymer length squared ~L2, in contrast to equilibrium counterparts ~L3. These insights offer prospects for designing new materials with activity-responsive mechanical properties.
Relevant publication
Press coverage

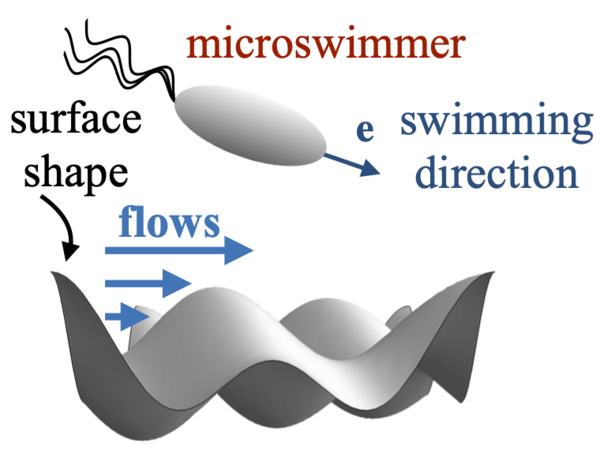
Swimming in confinement: Hydrodynamic couplings
We study hydrodynamic couplings and motion of microorganisms near elastic and corrugated surfaces using a combination of analytical and numerical methods.
Deformable boundaries are omnipresent in the habitats of swimming microorganisms, leading to intricate hydroelastic couplings. Employing a perturbation theory, valid for small deformations, we study the swimming dynamics of pushers and pullers near instantaneously deforming boundaries, endowed with a bending rigidity and surface tension. Our results reveal that pushers can both reorient away from the boundary, leading to overall hydroelastic scattering, or become trapped by the boundary, akin to the enhanced trapping found for pullers. These findings demonstrate that the complex hydroelastic interactions can generate behaviors that are in striking contrast to swimming near planar walls.
Relevant publications
Fluid-structure interactions in microfluidics
Flow through porous media
We study low-Reynolds-number fluid flow through a two-dimensional porous medium modeled as a Lorentz gas. Using extensive finite-element simulations we fully resolve the flow fields for packing fractions approaching the percolation threshold. Near the percolation transition, we find a power-law scaling of the flow rate versus the packing fraction with an exponent of ≈5/2, which was predicted earlier by mapping the macroscopic flow to a discrete flow network [B. I. Halperin et al., Phys. Rev. Lett. 54, 2391 (1985)]. Importantly, we observe a rounding of the scaling behavior at small system sizes, which can be rationalized via a finite-size scaling ansatz. Finally, we show that the distribution of the kinetic energy exhibits a power-law scaling over several decades at small energies, originating from collections of self-similar, viscous eddies in the dead-end channels. Our results lay the foundation for unraveling critical behavior of complex fluids omnipresent in biological and geophysical systems.
Relevant publication
Sedimentation and flows near structured surfaces: experiments & theory
Natural and microfluidic environments display a variety of confining surfaces with structured topographies, which modify the surrounding flow fields and and thereby impact the motion of nearby particles via hydrodynamic forces. We study the motion of spherical particles near corrugated surfaces, as are widely used in microfluidic applications, in low-Reynolds-number flows. Comparing quantitatively experiments and theory we show that spheres sedimenting near corrugated surfaces exhibit three-dimensional helical trajectories.
In addition to periodic, wavy surface structures, we study a non-Brownian spherical particle sedimenting nearby a random, rough surface by using an analytical theory and numerical simulations. Roughness of the wall induces fluctuations in the velocity of the fall, leading to a quadratic increase of the variance of the displacements at long times.
Relevant publications
J. Fluid Mech. 982, A31 (2024)
J. Phys.: Cond. Mat. 35, 274003 (2023)
Proc. Natl. Acad. Sci. U.S.A. 119, e2202082119 (2022)
Phys. Rev. Fluids 5, 082101(R) (2020)
Press coverage
Princeton pressA fluid interaction inspired a breakthrough in fluid dynamics
Statistical physics of semiflexible polymers
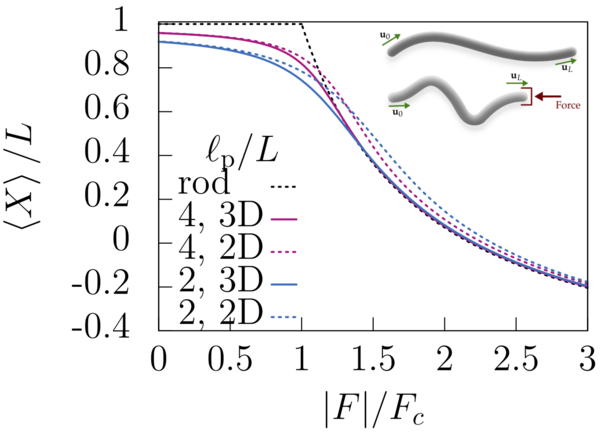
In addition to the dynamics of a self-propelled particle, the shape of its trajectory encodes interesting statistical physics and, in particular, is reminiscent of the contour of a semiflexible polymer, e.g., cytoskeletal filaments. Exploiting this analogy, we calculated analytically the experimentally accessible force-extension relations of semiflexible polymers both in 2D and in 3D, which demonstrates a continuous buckling behavior, in contrast to the Euler buckling instability of a rigid rod. We have also derived analytically the associated probability densities in 2D.
Relvant publications
Soft Matter 14, 7634 (2018)
Soft Matter 14, 2682 (2018)
Phys. Rev. E 95 (2017)