Topology and Correlations in Condensed Matter
Research
We are interested in a variety of problems in condensed matter theory. Our main focus lies on the study of phenomena which arise due to quantum mechanical effects in systems of correlated electrons. Areas of research include the study of topological phases of matter, fractional charges on geometrically frustrated lattices, and the applications of quantum information concepts to quantum many-body systems.
Below you can find short summaries of some of our recent research projects.
Characterization and stability of a fermionic ? = 1/3 fractional Chern insulator
Using the infinite density matrix renormalization group method on an infinite cylinder geometry, we characterize the 1/3 fractional Chern insulator state in the Haldane honeycomb lattice model at ? = 1/3 filling of the lowest band and check its stability. We investigate the chiral and topological properties of this state through (i) its Hall conductivity, (ii) the topological entanglement entropy, (iii) the U(1) charge spectral flow of the many body entanglement spectrum, and (iv) the charge of the anyons. In contrast to numerical methods restricted to small finite sizes, the infinite cylinder geometry allows us to access and characterize directly the metal to fractional Chern insulator tran- sition. We find indications it is first order and no evidence of other competing phases. Since our approach does not rely on any band or subspace projection, we are able to prove the stability of the fractional state in the presence of interactions exceeding the band gap, as has been suggested in the literature. As a by-product we discuss the signatures of Chern insulators within this technique.
Further reading:
A. G. Grushin, J. Motruk, M. P. Zaletel, and F. Pollmann, Phys. Rev. B 91, 035136 (2015).
Time-evolving a matrix product state with long-ranged interactions
We introduce a numerical algorithm to simulate the time evolution of a matrix product state under a long-ranged Hamiltonian. In the effectively one-dimensional representation of a system by matrix product states, long-ranged interactions are necessary to simulate not just many physical interactions but also higher- dimensional problems with short-ranged interactions. Since our method overcomes the restriction to short- ranged Hamiltonians of most existing methods, it proves particularly useful for studying the dynamics of both power-law interacting one-dimensional systems, such as Coulombic and dipolar systems, and quasi two- dimensional systems, such as strips or cylinders. First, we benchmark the method by verifying a long-standing theoretical prediction for the dynamical correlation functions of the Haldane-Shastry model. Second, we simu- late the time evolution of an expanding cloud of particles in the two-dimensional Bose-Hubbard model, a subject of several recent experiments.
Further reading:
Michael P. Zaletel, Roger S. K. Mong, Christoph Karrasch, Joel E. Moore, Frank Pollmann, arXiv:1407.1832 (2014).
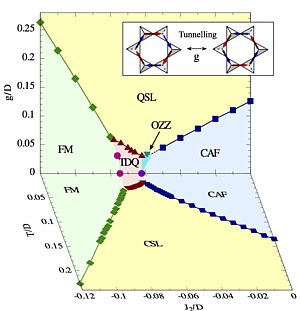
What is the quantum ground state of dipolar spin ice?
Recent experiments on the spin ice Dy2Ti2O7, suggest that the Pauling “ice entropy”, charac- teristic of its Coulombic spin-liquid state, may be lost at low temperatures [D. Pomaranski et al., Nature Phys. 9, 353 (2013)]. However, despite nearly two decades of intensive study, the nature of the equilibrium ground state of spin-ice remains uncertain. Here we explore how long-range dipolar interactions D, short-range exchange interactions and quantum fluctuations combine to determine the ground state of dipolar spin ice. We find that ordered ground states are selected from a set of “chain states” in which dipolar interactions are exponentially screened. Using both quantum and classical Monte Carlo simulation, we establish phase diagrams as a function of quantum tunneling g, and temperature T, and find that only a very small gc ? D is needed to stabilize a quantum spin-liquid ground state. We discuss the implications of these results for Dy2 Ti2 O7 , and for the “quantum spin ice” materials Yb2Ti2O7, Tb2Ti2O7 and Pr2Zr2O7.
Further reading:
Paul McClarty, Olga Sikora, Roderich Moessner, Karlo Penc, Frank Pollmann, Nic Shannon, arXiv:1410.0451 (2014).
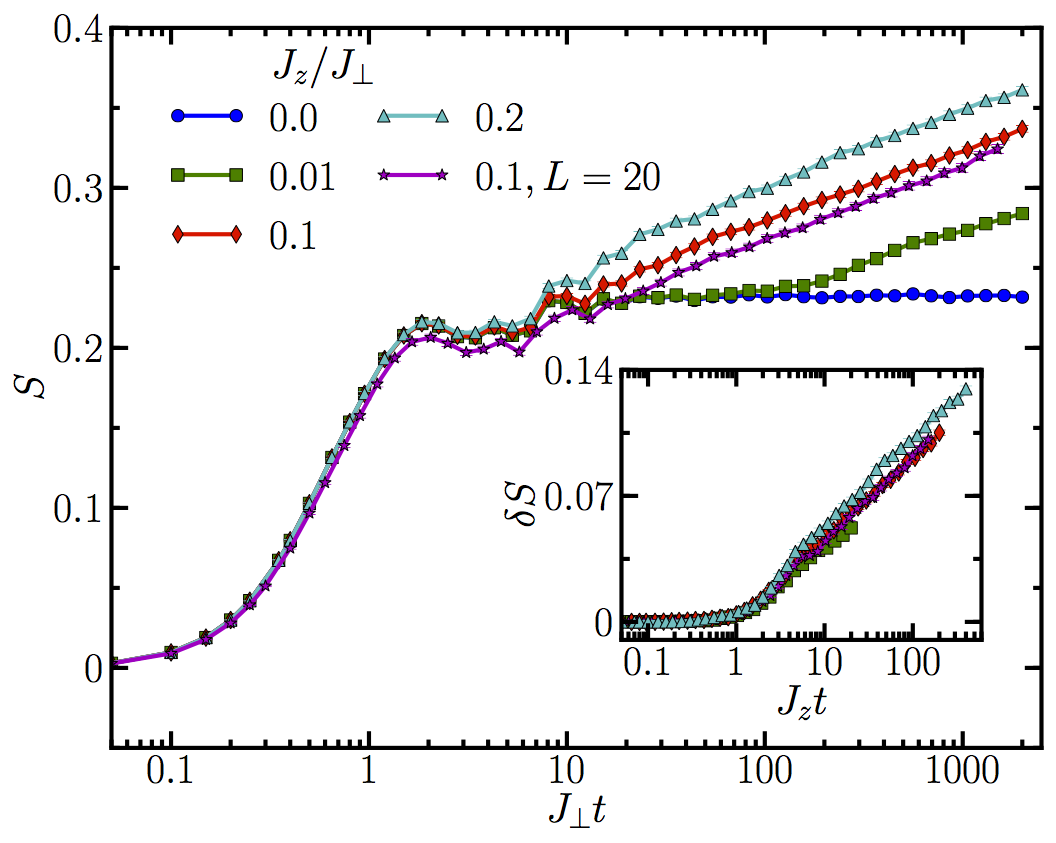
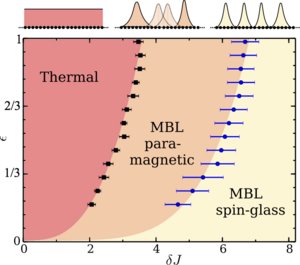
Many-body localization in a disordered quantum Ising chain
Many-body localization occurs in isolated quantum systems when Anderson localization persists in the pres- ence of finite interactions. Despite strong evidence for the existence of a many-body localization transition a reliable extraction of the critical disorder strength is difficult due to a large drift with system size in the studied quantities. In this work we explore two entanglement properties that are promising for the study of the many- body localization transition: the variance of the half-chain entanglement entropy of exact eigenstates and the long time change in entanglement after a local quench from an exact eigenstate. We investigate these quantities in a disordered quantum Ising chain and use them to estimate the critical disorder strength and its energy depen- dence. In addition, we analyze a spin-glass transition at large disorder strength and provide evidence for it being a separate transition. We thereby give numerical support for a recently proposed phase diagram of many-body localization with localization protected quantum order.
Further reading:
Jonas A. Kjall, Jens H. Bardarson, and Frank Pollmann,
arxiv:1403.1568 (2014).
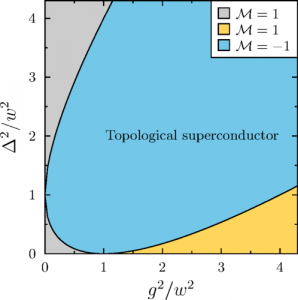
From fractionally charged solitons to Majorana bound states in a one-dimensional interacting model
We investigate the one dimensional Creutz model in the presence of induced superconductivity and Hubbard type interactions. We show that zero-energy Majorana edge modes develop in the presence of supeconducting pairing for a certain range of parameters. Additionally, the system hosts regular electronic zero-energy modes in a trivial superconducting phase. We study the effect of interactions using a combination of density matrix renormalization group (DRMG) methods and mean field theory. It is shown how local repulsive interactions expand the parameter range for which a topological Majorana phase is stabilized. In contrast, we find that interactions remove the zero-energy modes found in the trivial super conducting phase
Further reading:
Doru Sticlet, Luis Seabra, Frank Pollmann, and Jérôme Cayssol, Phys. Rev. B 89, 115430 (2014).
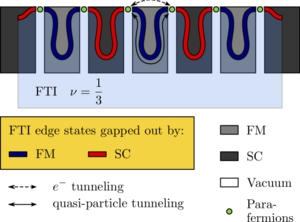
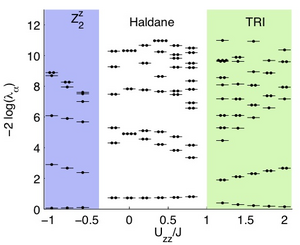
Topological Phases in gapped edges of fractionalized systems
We extend the classification scheme of topological phases in one-dimensional fermionic systems to parafermionic chains. In a series of recent works it had been shown that parafermions can arise on the edge of a two-dimensional fractional topological insulator when coupled to superconducting and ferromagnetic domains. The low-energy edge degrees of freedom are described by a chain of coupled parafermions. We discuss the classification of topological phases that can arise and study their entanglement. As a concrete example we consider the ? = 1/3 fractional topological insulator for which we calculate the phase diagram and study the entanglement spectra.
Further reading:
J. Motruk, A. M. Turner, E. Berg, Frank Pollmann, Phys. Rev. B 88, 085115 (2013).
Phase diagram of the isotropic spin-3/2 model on the z=3 Bethe lattice
We study an SU(2) symmetric spin-3/2 model on the z=3 Bethe lattice using the infinite Time Evolving Block Decimation (iTEBD) method. This model is shown to exhibit a rich phase diagram. We compute the expectation values of several order parameters which allow us to identify a ferromagnetic, a ferrimagnetic, a anti-ferromagnetic as well as a dimerized phase. We calculate the entanglement spectra from which we conclude the existence of a symmetry protected topological phase that is characterized by S=1/2 edge spins.
Further reading:
S. Depenbrock, F. Pollmann, Phys. Rev. B 88, 035138 (2013).
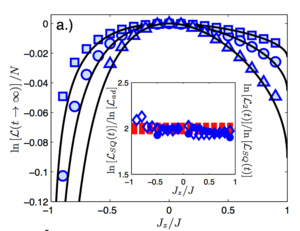
Loschmidt echo and the many-body orthogonality catastrophe in a qubit-coupled Luttinger liquid
We investigate the many-body generalization of the orthogonality catastrophe by studying the generalized Loschmidt echo of Luttinger liquids (LLs) after a global change of interaction.
It decays exponentially with system size and exhibits universal behaviour: the steady state exponent after quenching back and forth n-times between 2 LLs (bang-bang protocol) is 2n-times bigger than that of the adiabatic overlap, and depends only on the initial and final LL parameters. These are corroborated numerically by matrix-product state based methods of the XXZ Heisenberg model. An experimental setup consisting of a hybrid system containing cold atoms and a flux qubit coupled to a Feshbach resonance is proposed to measure the Loschmidt echo using rf spectroscopy or Ramsey interferometry.
Further reading:
B. Dóra, F. Pollmann, J. Fortágh, G. Zaránd, Phys. Rev. Lett. 111, 046402 (2013).
F. Pollmann, M. Haque, B. Dóra, Phys. Rev. B 87, 041109(R) (2013).
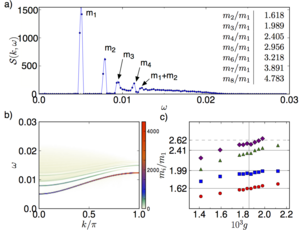
Exotic Ising dynamics in a Bose-Hubbard model
We explore the dynamical properties of a one-dimensional Bose-Hubbard model, where two different bosonic species interact via Feshbach resonance. We focus on the region in the phase diagram which is described by an effective, low-energy ferromagnetic Ising model in both transverse and longitudinal fields. In this regime, we numerically calculate the dynamical structure factor of the Bose-Hubbard model using the Time-Evolving Block Decimation method. In the ferromagnetic phase, we observe both the continuum of excitations and the bound states in the presence of a longitudinal field. Near the Ising critical point, we observe the celebrated E8 mass spectrum in the excited states. We also point out possible measurements which could be used to detect these excitations in an optical lattice experiment.
Further reading:
L. Seabra, F. Pollmann, Phys. Rev. B 88, 125103 (2013).
Topological characterization of fractional quantum Hall ground states from microscopic Hamiltonians
We show how to numerically calculate several quantities that characterize topological order starting from a microscopic fractional quantum Hall (FQH) Hamiltonian. To find the set of degenerate ground states, we employ the infinite density matrix renormalization group (iDMRG) method based on the matrix-product state (MPS) representation of FQH states on an infinite cylinder. To study localized quasiparticles of a chosen topological charge, we use pairs of degenerate ground states as boundary conditions for the iDMRG. We then show that the wave function obtained on the infinite cylinder geometry can be adapted to a torus of arbitrary modular parameter, which allows us to explicitly calculate the non-Abelian Berry connection associated with the modular T -transformation. As a result, the quantum dimensions, topological spins, quasiparticle charges, chiral central charge, and Hall viscosity of the phase can be obtained using data contained entirely in the entanglement spectrum of an infinite cylinder.
Further reading:
M. P. Zaletel, R. S. K. Mong, F. Pollmann, Phys. Rev. Lett. 110, 236801 (2013).
Michael P. Zaletel, Roger S. K. Mong, Frank Pollmann, and Edward H. Rezayi, Phys. Rev. B 91, 045115 (2015).
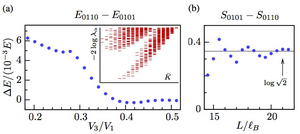
Detection of Symmetry Protected Topological Phases in 1D
A topological phase is a phase of matter which cannot be characterized by a local order param- eter. It has been shown that gapped phases in 1D systems can be completely characterized using tools related to projective representations of the symmetry groups.
We explain two ways to detect symmetry protected topological phases in 1D. First, we give a numerical approach how to directly extract the projective representations from a matrix-product state representation. Second, we de- rive non-local order parameters for time reversal, inversion symmetry, and discuss a generalized string-order for local symmetries for which the regular string-order parameter cannot be applied. We furthermore point out that the non-local order parameter for these topological phases is actually related to topological surfaces.
Further reading:
Frank Pollmann and Ari Turner, Phys. Rev. B 86, 125441 (2012).
Unbounded growth of entanglement in models of many-body localization
An important and incompletely answered question is whether a closed quantum system of many interacting particles can be localized by disorder. The time evolution of simple (unentangled) initial states is studied numerically for a system of interacting spinless fermions in one dimension described by the random-field XXZ Hamiltonian.
Interactions induce a dramatic change in the propagation of entanglement and a smaller change in the propagation of particles. For even weak interactions, when the system is thought to be in a many-body localized phase, entanglement shows neither localized nor diffusive behavior but grows without limit in an infinite system: interactions act as a singular perturbation on the localized state with no interactions. The significance for proposed atomic experiments is that local measurements will show a large but non-thermal entropy in the many-body localized state. This entropy develops slowly (approximately logarithmically) over a diverging time scale as in glassy systems.
Further reading:
Jens H. Bardarson, Frank Pollmann, Joel E. Moore, Phys. Rev. Lett. 109, 017202 (2012).
Quantum Ice: A Quantum Monte Carlo Study
Ice states, in which frustrated interactions lead to a macroscopic ground-state degeneracy, occur in water ice, in problems of frustrated charge order on the pyrochlore lattice, and in the family of rare-earth magnets collectively known as spin ice. Of particular interest at the moment are ‘‘quantum spin-ice’’ materials, where large quantum fluctuations may permit tunnelling between a macroscopic number of different classical ground states. Here we use zero-temperature quantum Monte Carlo simulations to show how such tunnelling can lift the degeneracy of a spin or charge ice, stabilizing a unique ‘‘quantum-ice’’ ground state— a quantum liquid with excitations described by the Maxwell action of 3+1 dimensional quantum electrodynamics. We further identify a competing ordered squiggle state, and show how both squiggle and quantum-ice states might be distinguished in neutron scattering experiments on a spin-ice material.
Further reading:
N. Shannon, O. Sikora, F. Pollmann, K. Penc, and Peter Fulde, Phys. Rev. Lett. 108, 067204 (2012).
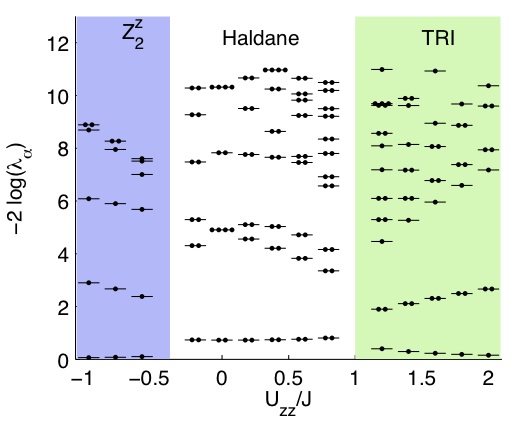
Topological phases in one dimension: An Entanglement Point of View
A topological phase is a phase of matter which cannot be characterized by a local order parameter, and thus falls beyond the Landau paradigm of condensed matter physics.
An example of a symmetry protected topological ph
ase is the Haldane phase of S = 1 chains. Here we found that the entire phase is characterized by a double degeneracy of the entanglement spectrum (see figure). The degeneracy is protected by a set of symmetries (either the dihedral group of ?-rotations about two orthogonal axes, time-reversal symmetry, or bond centered inversion symmetry), and cannot be lifted unless either a phase boundary to another, “topologically trivial”, phase is crossed, or the symmetry is broken. More generally, these results offer a scheme to classify gapped phases of one dimensional systems.
In a second application, we focus on one-dimensional fermionic systems. The effect of interactions on topological insulators and superconductors remains, to a large extent, an open problem. Here, we developed a framework for classifying phases of one-dimensional interacting fermions, focusing on spinless fermions with time-reversal symmetry and particle number parity conservation. In agreement with an example presented by Fidkowski et al., we find that in the presence of interactions there are only eight distinct phases, which obey a Z8 group structure. This is in contrast to the Z classification in the non-interacting case. Each of these eight phases is characterized by a unique set of bulk invariants, related to the transformation laws of its entanglement (Schmidt) eigenstates under symmetry operations, and has a characteristic degeneracy of its entanglement levels.
Further reading:
F. Pollmann, A.M. Turner, E. Berg, and M. Oshikawa, Phys. Rev. B 81, 064439 (2010).
A.M. Turner, F. Pollmann, E. Berg, Phys. Rev. B 83, 075102 (2011).
F. Pollmann, E. Berg, A. M. Turner, and M. Oshikawa, Phys. Rev. B 85, 075125 (2012).
J. A. Kjäll, M. P. Zaletel, R. S. K. Mong, J. H. Bardarson, and F. Pollmann, Phys. Rev. B 87, 235106 (2013).
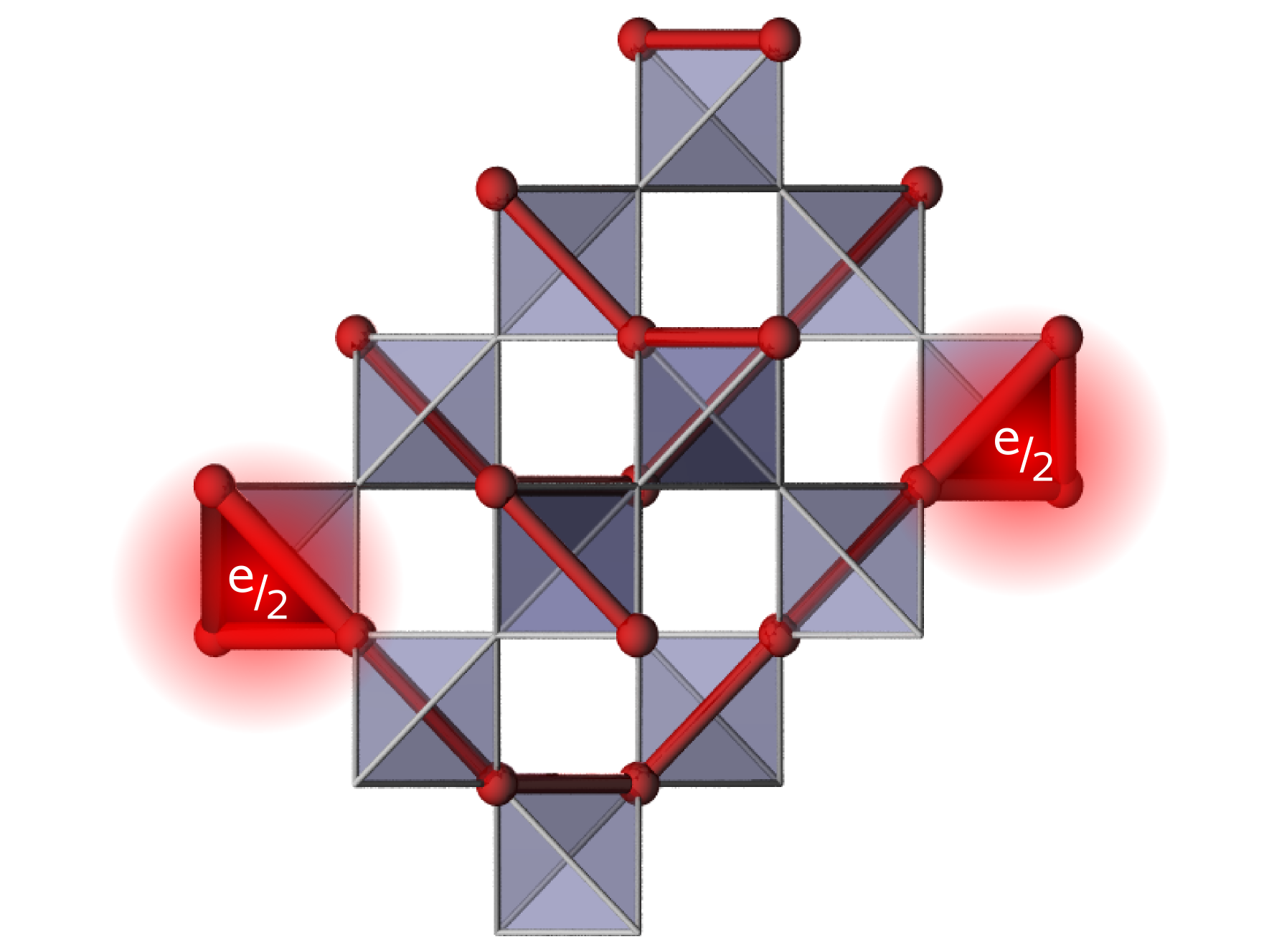
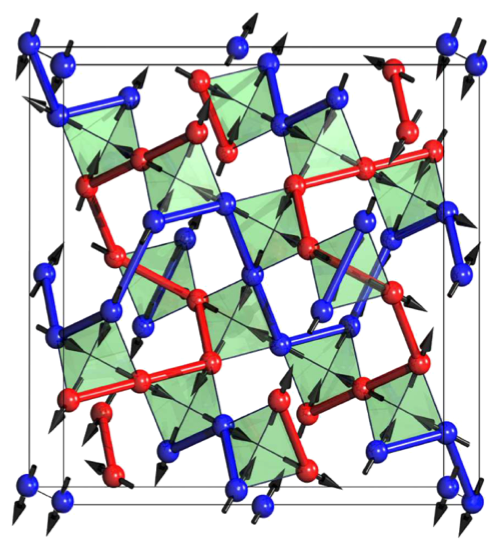
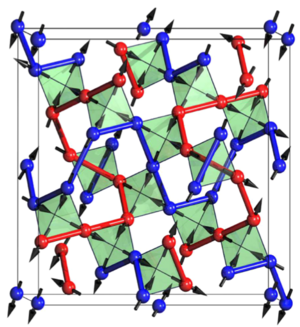
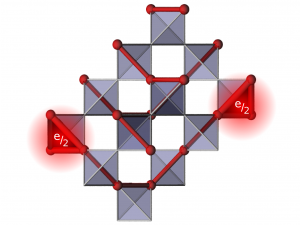
Charge degrees of freedom on frustrated lattices
After the discovery of the FQHE, the question was left open whether fractionally charged excitations could exist in three-dimensions. In 2002, it was suggested by Fulde, Penc and Shannon that excitations with charge e/2 could exist in a model of strongly correlated fermions on certain frustrated lattices, e.g, the three-dimensional pyrochlore lattice and its two-dimensional projection, the checkerboard lattice (see figure).
We used exact diagonalization methods to study the two-dimensional version of the pyrochlore lattice (i.e., the checkerboard lattice) and showed that fractional charges are linearly confined. The confinement results from a reduction of vacuum fluctuations and a polarization of the vacuum in the vicinity of a connecting string. The spectral functions show broad low-energy excitations which are due to the dynamics of fractionally charged excitations. Signatures for quasiparticles with large spatial extent are found (bound pairs of two fractionally charged particles). An effective low-energy Hamiltonian can be mapped to a U(1) lattice gauge theory which relates the considered low-energy model to the compact quantum electrodynamics in 2+1 dimensions.
For an effective low-energy model for the (three-dimensional) pyrochlore lattice, we showed that a U(1)-liquid phase with fractionalized excitations can be stabilized for a certain range of parameters using large scale quantum Monte Carlo methods. The U(1) phase exhibits transverse excitations with a linear dispersion (“photons”) and the mutual interaction between electric charges falls of as in Coulomb’s law.
Further reading:
F. Pollmann, Joseph J. Betouras, Kirill Shtengel, Peter Fulde, Phys. Rev. B 83, 155117 (2011).
O. Sikora, F. Pollmann, N. Shannon, K. Penc, and P. Fulde, Phys. Rev. Lett. 103, 247001 (2009).
F. Pollmann, E. Runge, and P. Fulde, Phys. Rev. B 73, 125121 (2006).
F. Pollmann, J. J. Betouras, K. Shtengel, and ?P. Fulde, Phys. Rev. Lett. 97, 170407 (2006).
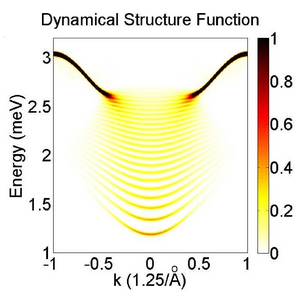
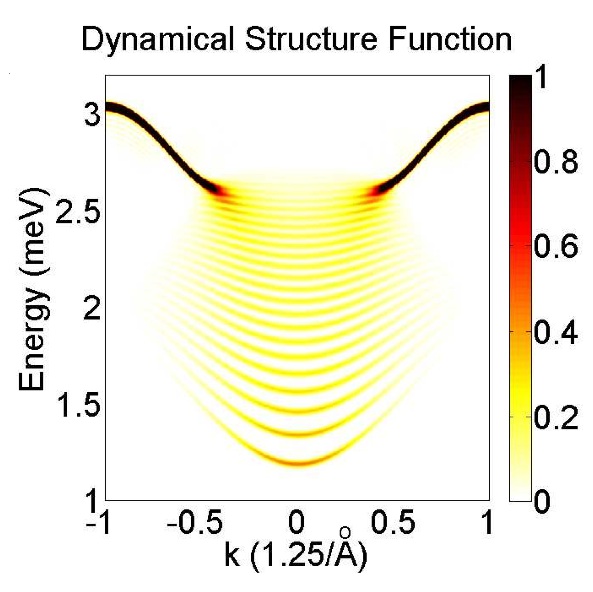
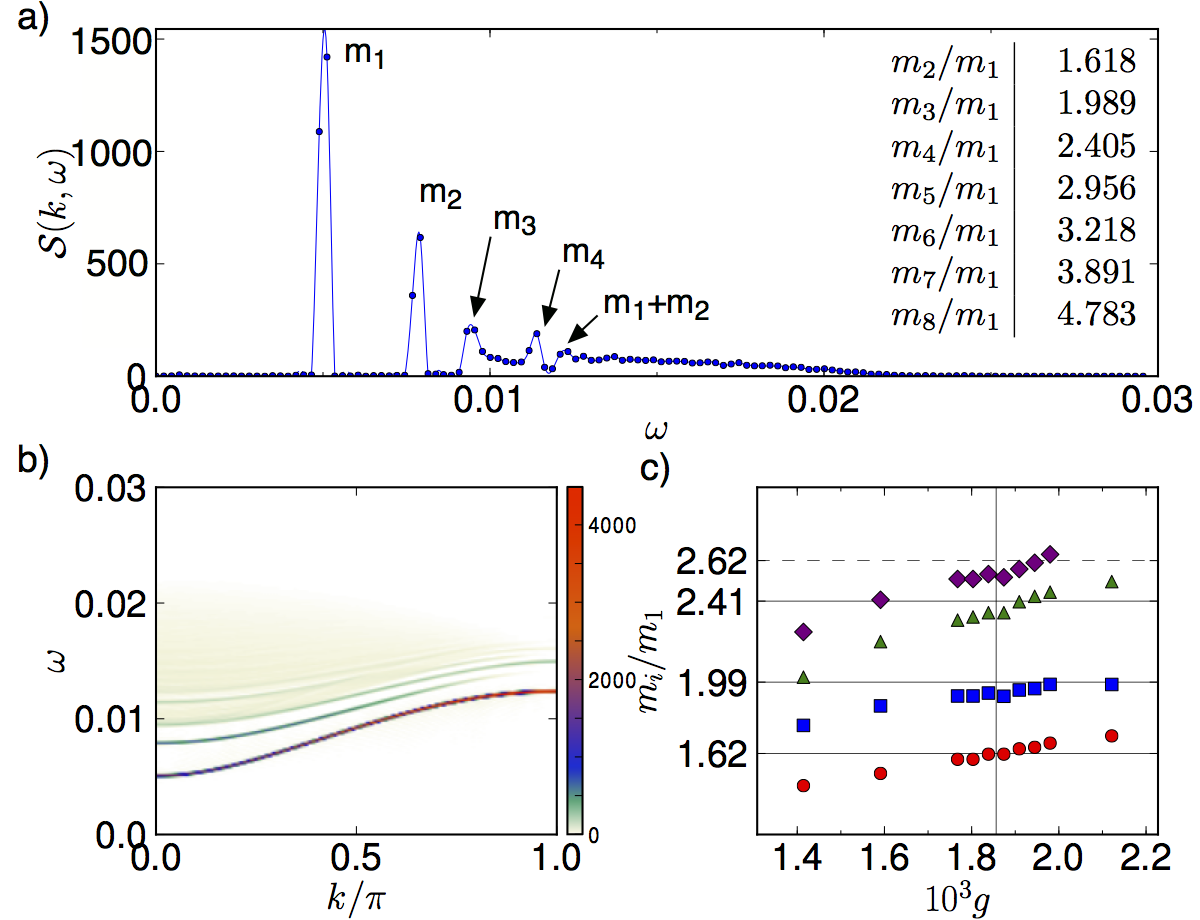
Bound states and E8 symmetry effects in perturbed quantum Ising chains
In a recent experiment on CoNb2O6, Coldea et al. found for the first time experimental evidence of the exceptional Lie algebra E8. The emergence of this symmetry was theoretically predicted long ago for the transverse quantum Ising chain in the presence of a weak longitudinal field.
We consider an accurate microscopic model of CoNb2O6 incorporating additional couplings and calculate numerically the dynamical structure factor (see figure) using a recently developed Time evolving block decimation (TEBD) method. The TEBD method provides an efficient method to perform a time evolution of quantum states in one-dimensional systems. It can be seen as a descendant of the density matrix renormalization group method and is based on a matrix product state (MPS) representation of the wave- functions. Algorithms of this type are efficient because they exploit the fact that the ground-state wave functions are only slightly entangled, especially away from criticality. As the entanglement grows linearly as a function of time, the simulations of long time evolutions is numerically very difficult. The excitation spectra show bound states characteristic of the weakly broken E8 symmetry. We compare the observed bound state signatures in this model to those found in the transverse Ising chain in a longitudinal field and to experimental data.
Further reading:
J.A. Kjäll, F. Pollmann, J.E. Moore, Phys. Rev. B 83, 020407 (2011).