
Accepted “as is”
Asymptotic densities of ballistic Levy walks
Our paper on asymptotic properties of Random walks was published in Phys. Rev. E
Asymptotic densities of ballistic Levy walks
by D. Froemberg, M. Schmiedeberg, E. Barkai, and V. Zaburdaev
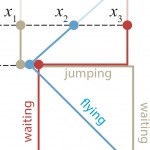
Abstract
We propose an analytical method to determine the shape of density profiles in the asymptotic long-time limit for a broad class of coupled continuous-time random walks which operate in the ballistic regime. In particular, we show that different scenarios of performing a random-walk step, via making an instantaneous jump penalized by a proper waiting time or via moving with a constant speed, dramatically effect the corresponding propagators, despite the fact that the end points of the steps are identical. Furthermore, if the speed during each step of the random walk is itself a random variable, its distribution gets clearly reflected in the asymptotic density of random walkers. These features are in contrast with more standard nonballistic random walks.
See Publications page for the full paper.
(February 23, 2015)