Research Highlights
You can learn more about the recent projects in the group below. For more details, check out our publications.
Geometric Floquet theory
Paul Manuel Schindler, Marin Bukov
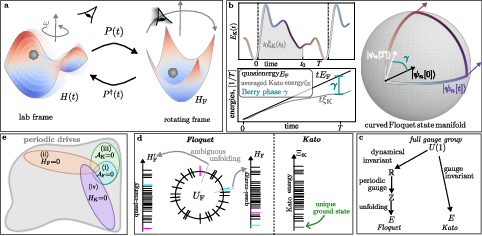
We derive Floquet theory from quantum geometry. We identify quasienergy folding as a consequence of a broken gauge group of the adiabatic gauge potential U(1)↦ℤ. This allows us to introduce a unique gauge-invariant formulation, decomposing the dynamics into a purely geometric and a purely dynamical evolution. The dynamical Kato operator provides an unambiguous sorting of the quasienergy spectrum, identifying a unique Floquet ground state and suggesting a way to define the filling of Floquet-Bloch bands. We exemplify the features of geometric Floquet theory using an exactly solvable XY model and a non-integrable kicked Ising chain; we show that the geometric contribution to the evolution accounts for inherently nonequilibrium effects, like the π-quasienergy gap in discrete time crystals or edge modes in anomalous Floquet topological insulators. The spectrum of the Kato operator elucidates the origin of both heating and spatiotemporal symmetry-breaking transitions. Last, we demonstrate that the periodic lab frame Hamiltonian generates transitionless counterdiabatic driving for Floquet eigenstates; this enables the direct application of shortcuts-to-adiabaticity techniques to Floquet engineering, turning it into an explicit algorithmic procedure. This work directly bridges seemingly unrelated areas of nonequilibrium physics. arXiv:2410.07029
Topological phase transitions in a constrained two-qubit quantum control landscape
Nicolò Beato, Pranay Patil, Marin Bukov
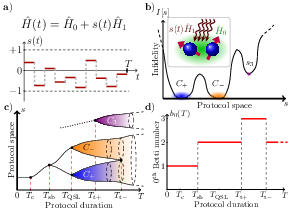
In optimal quantum control, control landscape phase transitions (CLPTs) indicate sharp changes occurring in the set of optimal protocols, as a physical model parameter is varied. Here, we demonstrate the existence of a new class of CLPTs, associated with changes in the topological properties of the optimal level set in a two-qubit state-preparation problem. In particular, the distance distribution of control protocols sampled through stochastic homotopic dynamics reveals discontinuous changes in the number of connected components in the optimal level set, as a function of the protocol duration. We demonstrate how topological CLPTs can be detected in modern-day experiments. arXiv:2411.08736
Discrete Time Crystal Sensing
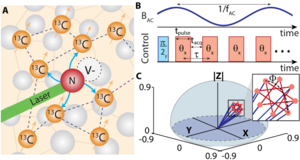
Leo Joon Il Moon, Paul M. Schindler, Ryan J. Smith, Emanuel Druga, Zhuo-Rui Zhang, Marin Bukov, Ashok Ajoy
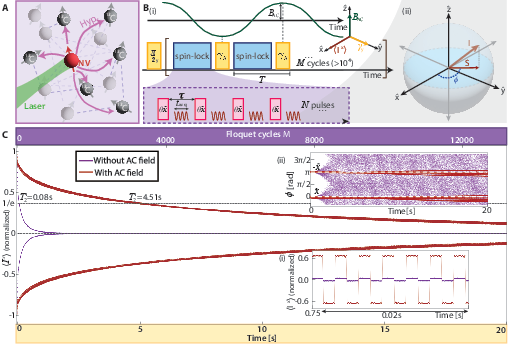
Prethermal discrete time crystals (PDTCs) are a nonequilibrium state of matter characterized by long-range spatiotemporal order, and exhibiting a subharmonic response stabilized by many-body interactions under periodic driving. The inherent robustness of time crystalline order to perturbations in the drive protocol makes DTCs promising for applications in quantum technologies. We exploit the susceptibility of PDTC order to deviations in its order parameter to devise highly frequency-selective quantum sensors for time-varying (AC) magnetic fields in a system of strongly-driven, dipolar-coupled 13C nuclear spins in diamond. Integrating a time-varying AC field into the PDTC allows us to exponentially increase its lifetime, measuring improvement of up to three orders of magnitude (44,204 cycles), and results in a strong resonant response in the time crystalline order parameter. The linewidth of our sensor is limited by the PDTC lifetime alone, as strong interspin interactions help stabilize DTC order. The sensor operates in the 0.5-50 kHz range - a blind spot for sensors based on atomic vapor or electronic spins - and attains a competitive sensitivity. PDTC sensors are resilient to errors in the drive protocol and sample inhomogeneities, and are agnostic to the macroscopic details of the physical platform: the underlying physical principle applies equally to superconducting qubits, neutral atoms, and trapped ions. arXiv:2410.05625
Floquet-engineered Emergent Massive Nambu-Goldstone Modes
Yang Hou, Zhanpeng Fu, Roderich Moessner, Marin Bukov, Hongzheng Zhao
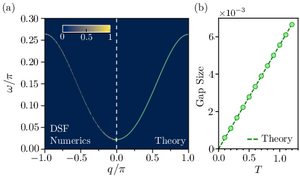
We present a general framework to implement massive Nambu-Goldstone quasi-particles in driven many-body systems. The underlying mechanism leverages an explicit Lie group structure imprinted into an effective Hamiltonian that governs the dynamics of slow degrees of freedom; the resulting emergent continuous symmetry is weakly explicitly broken, giving rise to a massive Nambu-Goldstone mode, with a spectral mass gap scaling linearly with the drive period. We discuss explicit and experimentally implementable realizations, such as Heisenberg-like spin models that support gapped spin-wave excitations. We provide a protocol to certify the existence of the massive Nambu-Goldstone mode from the dynamics of specific observables, and analyse the dispersion spectrum and their lifetime in the presence of weak explicit symmetry breaking. arXiv:2409.01902
Counterdiabatic Driving for Periodically Driven Systems
Paul Manuel Schindler, Marin Bukov
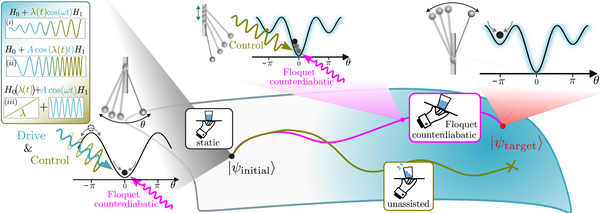
Periodically driven systems have emerged as a useful technique to engineer the properties of quantum systems, and are in the process of being developed into a standard toolbox for quantum simulation. An outstanding challenge that leaves this toolbox incomplete is the manipulation of the states dressed by strong periodic drives. The state-of-the-art in Floquet control is the adiabatic change of parameters. Yet, this requires long protocols conflicting with the limited coherence times in experiments. To achieve fast control of nonequilibrium quantum matter, we generalize the notion of variational counterdiabatic driving away from equilibrium focusing on Floquet systems. We derive a nonperturbative variational principle to find local approximations to the adiabatic gauge potential for the effective Floquet Hamiltonian. It enables transitionless driving of Floquet eigenstates far away from the adiabatic regime. We discuss applications to two-level, Floquet band, and interacting periodically-driven models. The developed technique allows us to capture non-perturbative photon resonances and obtain high-fidelity protocols that respect experimental limitations like the locality of the accessible control terms. arXiv:2310.02728
Reinforcement Learning to Disentangle Multiqubit Quantum States from Partial Observations
Pavel Tashev, Stefan Petrov, Friederike Metz, Marin Bukov
Using partial knowledge of a quantum state to control multiqubit entanglement is a largely unexplored paradigm in the emerging field of quantum interactive dynamics with the potential to address outstanding challenges in quantum state preparation and compression, quantum control, and quantum complexity. We present a deep reinforcement learning (RL) approach to constructing short disentangling circuits for arbitrary 4-, 5-, and 6-qubit states using an actor-critic algorithm. With access to only two-qubit reduced density matrices, our agent decides which pairs of qubits to apply two-qubit gates on; requiring only local information makes it directly applicable on modern NISQ devices. Utilizing a permutation-equivariant transformer architecture, the agent can autonomously identify qubit permutations within the state, and adjusts the disentangling protocol accordingly. Once trained, it provides circuits from different initial states without further optimization. We demonstrate the agent's ability to identify and exploit the entanglement structure of multiqubit states. For 4-, 5-, and 6-qubit Haar-random states, the agent learns to construct disentangling circuits that exhibit strong correlations both between consecutive gates and among the qubits involved. Through extensive benchmarking, we show the efficacy of the RL approach to find disentangling protocols with minimal gate resources. We explore the resilience of our trained agents to noise, highlighting their potential for real-world quantum computing applications. Analyzing optimal disentangling protocols, we report a general circuit to prepare an arbitrary 4-qubit state using at most 5 two-qubit (10 CNOT) gates. arXiv:2406.07884 github repository
Experimental observation of a time rondeau crystal: Temporal Disorder in Spatiotemporal Order
Leo Joon Il Moon, Paul Manuel Schindler, Yizhe Sun, Emanuel Druga, Johannes Knolle, Roderich Moessner, Hongzheng Zhao, Marin Bukov, Ashok Ajoy
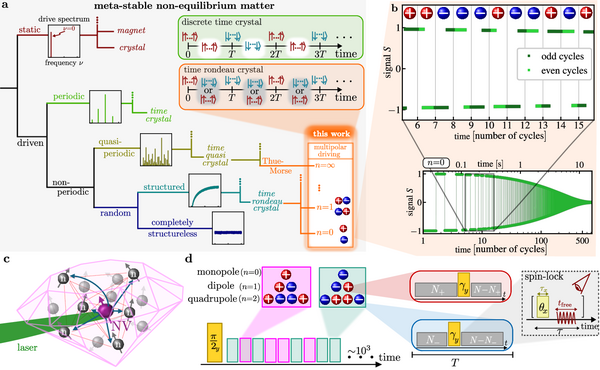
Our understanding of phases of matter relies on symmetry breaking, one example being water ice whose crystalline structure breaks the continuous translation symmetry of space. Recently, breaking of time translation symmetry was observed in systems not in thermal equilibrium. The associated notion of time crystallinity has led to a surge of interest, raising the question about the extent to which highly controllable quantum simulators can generate rich and tunable temporal orders, beyond the conventional classification of order in static systems. Here, we investigate different kinds of partial temporal orders, stabilized by non-periodic yet structured drives, which we call rondeau order. Using a 13C-nuclear-spin diamond quantum simulator, we report the first experimental observation of a -- tunable degree of -- short-time disorder in a system exhibiting long-time stroboscopic order. This is based on a novel spin control architecture that allows us to implement a family of drives ranging from structureless via structured random to quasiperiodic and periodic drives. Leveraging a high throughput read-out scheme, we continuously observe the spin polarization over 105 pulses to probe rondeau order, with controllable lifetimes exceeding 4 seconds. Using the freedom in the short-time temporal disorder of rondeau order, we show the capacity to encode information in the response of observables. Our work broadens the landscape of observed nonequilibrium temporal order, paving the way for new applications harnessing driven quantum matter. arXiv:2404.05620
Engineering Hierarchical Symmetries
Zhanpeng Fu, Roderich Moessner, Hongzheng Zhao, Marin Bukov
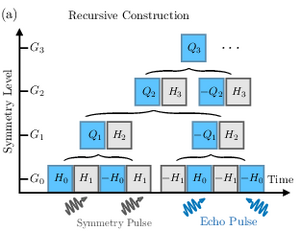
We present a general driving protocol for many-body systems to generate a sequence of prethermal regimes, each exhibiting a lower symmetry than the preceding one. We provide an explicit construction of effective Hamiltonians exhibiting these symmetries. This imprints emergent quasi-conservation laws hierarchically, enabling us to engineer the respective symmetries and concomitant orders in nonequilibrium matter. We provide explicit examples, including spatiotemporal and topological phenomena, as well as a spin chain realizing the symmetry ladder SU(2)→U(1)→ℤ2→E. arXiv:2402.13519
Nonequilibrium phononic first-order phase transition in a driven fermion chain
Mohsen Yarmohammadi, Marin Bukov, Michael H. Kolodrubetz
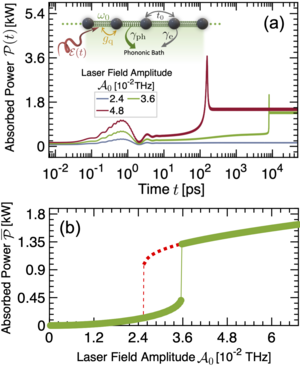
We study the direct laser drive of infrared-active phonons that are quadratically coupled to a spinless fermion chain. Feedback is incorporated by phonon dressing of the electronic dispersion, which enables effective non-linearities in the phonon dynamics. We uncover a first-order phase transition in the phononic steady state in which hysteretic effects allow either large or small phonon occupation depending on the drive protocol. We discuss the implications of these findings for probing phase transitions in real driven materials. Our findings motivate future nonequilibrium spectroscopy experiments to seek photo-induced phononic phase transitions in driven quantum materials such as driven superconductors, where the modified phononic steady state may enable a nonequilibrium pathway to controlling superconductivity. This phase transition will likely also be possible in the presence of an electromagnetic cavity, which has been used in recent work to control heating in driven materials. arXiv:2304.12962
Engineering and probing non-Abelian chiral spin liquids using periodically driven ultracold atoms
Bo-Ye Sun, Nathan Goldman, Monika Aidelsburger, Marin Bukov
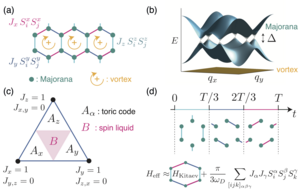
We propose a scheme to implement Kitaev's honeycomb model with cold atoms, based on a periodic (Floquet) drive, in view of realizing and probing non-Abelian chiral spin liquids using quantum simulators. We derive the effective Hamiltonian to leading order in the inverse-frequency expansion, and show that the drive opens up a topological gap in the spectrum without mixing the effective Majorana and vortex degrees of freedom. We address the challenge of probing the physics of Majorana fermions, while having only access to the original composite spin degrees of freedom. Specifically, we propose to detect the properties of the chiral spin liquid phase using gap spectroscopy and edge quenches in the presence of the Floquet drive. The resulting chiral edge signal, which relates to the thermal Hall effect associated with neutral Majorana currents, is found to be robust for realistically-prepared states. By combining strong interactions with Floquet engineering, our work paves the way for future studies of non-Abelian excitations and quantized thermal transport using quantum simulators. arXiv:2211.09777
'Prethermalization' in Conservative Nonsymplectic Periodically Driven Spin Systems
Adam J. McRoberts, Hongzheng Zhao, Roderich Moessner, Marin Bukov
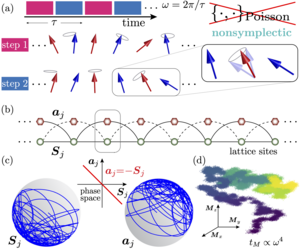
We analyze a new class of time-periodic dynamics in interacting chaotic classical spin systems, whose equations of motion are conservative (phase-space volume preserving) yet possess no symplectic structure. As a result, the dynamics of the system cannot be derived from any time-dependent Hamiltonian. In the high-frequency limit, we find that the magnetization dynamics features a long-lived metastable plateau, whose duration is controlled by the fourth power of the drive frequency. However, due to the lack of an effective Hamiltonian, the system does not evolve into a strictly prethermal state. We propose a Hamiltonian extension of the system using auxiliary degrees of freedom, in which the original spins constitute an open yet nondissipative subsystem. This allows us to perturbatively derive effective equations of motion that manifestly display symplecticity breaking at leading order in the inverse frequency. We thus extend the notion of prethermal dynamics, observed in the high-frequency limit of periodically-driven systems, to a nonsymplectic setting. arXiv:2208.09005
Verification of the Quantum Jarzynski Equality on Digital Quantum Computers
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, Marin Bukov
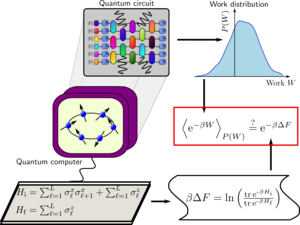
The quantum Jarzynski equality and the Crooks relation are fundamental laws connecting equilibrium processes with nonequilibrium fluctuations. While they are well established theoretically and also experimental realizations for simple few-body systems already exist, a verification in the quantum many-body regime is still missing. Closing this gap becomes crucial in the light of the rapid development of quantum technologies, since it represents a natural test for the validity of the laws of quantum thermodynamics in closed systems, on the one side, and the utility of modern quantum simulators to reveal and scrutinize fundamental principles of nature, on the other. We verify the quantum Jarzynski equality and the Crooks relation in systems with up to sixteen interacting qubits on digital quantum computers. We overcome present-day limitations in the preparation of thermal ensembles and in the measurement of work distributions. Our analysis reveals a novel dissipative nonequilibrium regime, where a fast unitary drive compensates for dissipation and restores the validity of Jarzynski's equality.
Continuously tracked, stable, large excursion trajectories of dipolar coupled nuclear spins
Ozgur Sahin, Hawraa Al Asadi, Paul Schindler, Arjun Pillai, Erica Sanchez, Matthew Markham, Mark Elo, Maxwell McAllister, Emanuel Druga, Christoph Fleckenstein, Marin Bukov, Ashok Ajoy
Periodically driven (Floquet) quantum systems have become a paradigm for their capability to engineer and sustain stable long-lived states where energy absorption can be controllably suppressed. However, this approach is often restricted to specific initial states, typically aligned parallel to the driving field. In collaboration with Ajoy lab at UC Berkeley, we propose the engineering of robust closed spin orbits on the Bloch sphere. Our approach combines micromotion, which enables the engineering of a time-periodic family of Hamiltonians, with key concepts from the eigenstate thermalisation hypothesis, and Floquet pre-thermalisation. Our idea is experimentally demonstrated in a model system of long-range strongly interacting C13 nuclear spins in diamond with an intrinsic decoherence time of 1.5 ms. Using dynamical stabilisation we demonstrate the ability to excite and track robust designer trajectories for a lifetime of tens of seconds, corresponding to an increase in decoherence time of more than 4 orders of magnitude. Our results suggest new ways to stabilise strongly-coupled quantum systems through periodic driving, and portend powerful applications of rigid spin orbits in quantum sensing.
Monte Carlo Tree Search based Hybrid Optimization of Variational Quantum Circuits
Jiahao Yao, Haoya Li, Marin Bukov, Lin Lin, Lexing Ying
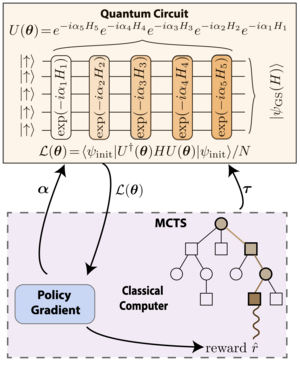
Variational quantum algorithms stand at the forefront of simulations on near-term and future fault-tolerant quantum devices. While most variational quantum algorithms involve only continuous optimization variables, the representational power of the variational ansatz can sometimes be significantly enhanced by adding discrete optimization variables, as is exemplified by the generalized quantum approximate optimization algorithm (QAOA). However, the hybrid discrete-continuous optimization problem poses a challenge for optimization. In collaboration with the Lin group at UC Berkeley and the Ying group at Stanford, we propose a new algorithm called MCTS-QAOA, which combines a Monte Carlo tree search method with an improved natural policy gradient solver to optimize the discrete and continuous variables in the quantum circuit. MCTS-QAOA has excellent noiseresilience properties and outperforms prior algorithms.
Self-Correcting Quantum Many-Body Control using Reinforcement Learning with Tensor Networks
Friederike Metz, Marin Bukov
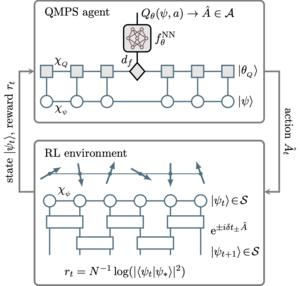
Quantum simulators and computers require optimal control techniques for state preparation. At the same time, the number of qubits is increasing at a rapid rate which poses a challenge for finding optimal control strategies in the many-body regime. We propose a novel approach for controlling quantum many-body systems based on reinforcement learning. The quantum many-body problem is tackled by leveraging matrix product states for both representing the quantum system and as a trainable deep learning ansatz for the reinforcement learning agent. The framework allows us to reach far larger system sizes than approaches based purely on neural networks while retaining the general advantages of deep learning methods such as generalizability and robustness to noise. We demonstrate that our agent can perform universal state preparation for a small number of spins, control a many-body spin chain of N=32 sites, and prepare ground states in the critical region of the Ising model. Our work opens up the door to further research at the intersection of tensor network-based machine learning and reinforcement learning.
Observation of a critical prethermal discrete time crystal created by two-frequency driving
William Beatrez, Christoph Fleckenstein, Arjun Pillai, Erica Sanchez, Amala Akkiraju, Jesus Alcala, Sophie Conti, Paul Reshetikhin, Emanuel Druga, Marin Bukov, Ashok Ajoy
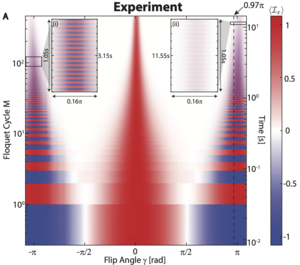
In collaboration with the Ajoy lab at UC Berkeley, we observed long-lived Floquet prethermal discrete time crystalline (PDTC) order in a three-dimensional position-disordered lattice of interacting dipolar-coupled 13C nuclei in diamond. We demonstrate a novel strategy of "two-frequency" driving, involving an interleaved application of slow and fast drives that simultaneously prethermalize the spins with an emergent quasi-conserved magnetization along the x-axis, while enabling continuous and highly resolved observation of their dynamic evolution when periodically kicked away from x. The PDTC order manifests itself in a robust period doubling response of this drive-induced quasi-conserved spin magnetization interchanging between x and -x. We obtain movies of the time-crystalline response with a clarity and throughput orders of magnitude greater than previous experiments. Such rapid measurement enables detailed characterization of the entire PDTC phase diagram, rigidity and lifetime, informing on the role of prethermalization towards stabilizing the DTC response.
Check out our preprint arXiv:2201.02162