Research
Research
We study the interplay of strong interactions, fractionalization and topology, specially in gapless phases of matter. We also study unconventional forms of spin and charge charge transport. Our problems are often experimentally inspired.
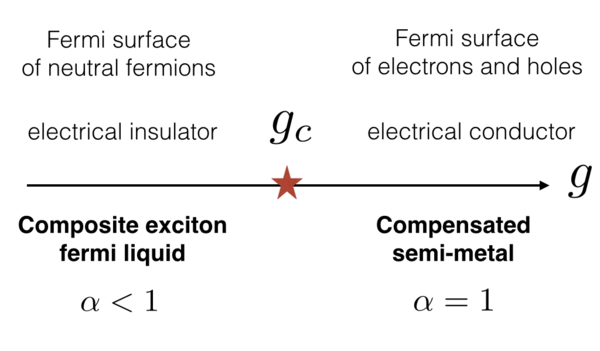
Neutral Fermi Surfaces in Electrical Insulators
We have recently proposed a new phase for mixed valence insulators motivated by the intriguing observations in SmB6. This phase, which we call the "composite exciton fermi liquid", has a fermi surface of emergent neutral fermions minimally coupled to an emergent U(1) gauge field. It is an insulator to electric charge but can conduct heat like a metal and displays an analogue of the de-Haas van Alphen effect.
Quantum Hall Ferroelectrics and Nematics
We have proven a generalized version of quantum Hall ferromagnetism in which a wide class of multi-valley quantum Hall systems at integer filling lead to spontaneously broken symmetry states that break spontaneously inversion and/or rotation symmetries.
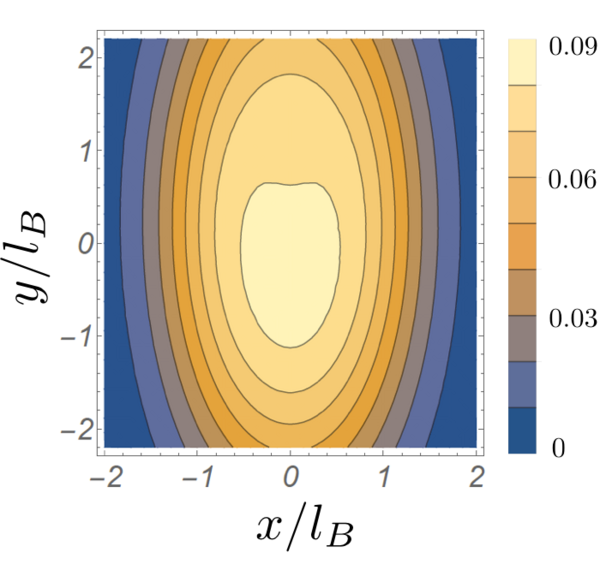
Transition from Moore-Read State to Quantum Hall Stripes
We have also recently studied the phase transition from the Moore-Read state to the stripe charge density wave state driven by mass anisotropy.
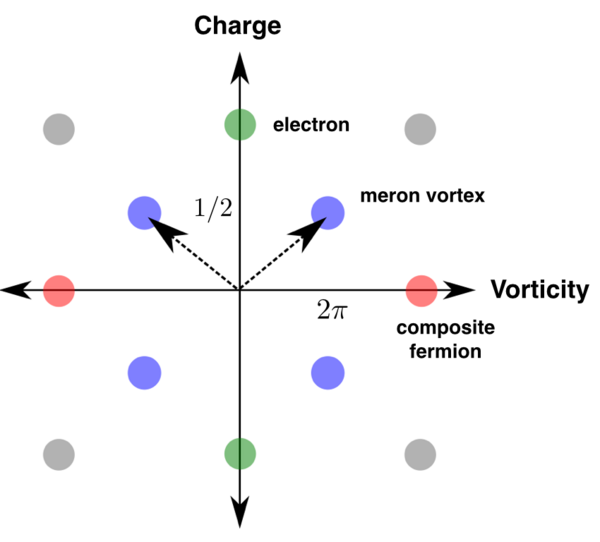
Exciton condensation equals Composite fermion pairing
We have discovered a remarkable connection between two well known fractionalized phases of matter: "the exciton condensate" realized in quantum Hall bilayers and the "composite fermi liquid" state realized in half-filled Landau levels. We found that there exists a special interlayer pairing channel for composite fermions that is identical to the exciton condensate, so that both states can be adiabatically connected in a manner analogous to the BEC to BCS crossover.