
Research
Topology on fractal lattices and quasicrystals
We investigate how the properties of quantum systems are affected by modifying the space on which the models are defined. In particular, we study quantum systems on lattices in fractal dimensions, quasicrystals, and disordered systems.
We have, e.g., shown that the fractional quantum Hall effect is not specific to two dimensions, but can also appear in fractal dimensions [1]. We have also studied the role of the coordination number for topological systems on fractal lattices [2] and topological models on quasicrystals [3].
[1] PRResearch 2, 023401 (2020), PRA 105, L021302 (2022), PRB 105, 085152 (2022)
[2] PRB 104, 045147 (2021)
[3] PRB 101, 115413 (2020)
Nonthermal quantum systems
Closed quantum systems typically thermalize by following the eigenstate thermalization hypothesis. There are, however, examples of quantum systems that do not thermalize, and these are interesting due to their unusual properties and ability to preserve quantum information. Many-body localization is an example of a strong violation of the eigenstate thermalization hypothesis, in which all states in the spectrum are nonthermal, and quantum many-body scars are examples of weak violations, in which only a few states are nonthermal.
We have proposed a different type of nonthermal system, which realizes a weak violation of many-body localization by embedding a critical state into a spectrum of many-body localized states [1]. We have also constructed and analyzed different types of quantum many-body scars with topological order [2].
[1] PRL 125, 240401 (2020)
[2] PRB 104, L121103 (2021), PRB 102, 235106 (2020)

Anyons
Anyons are quasiparticles that can appear in topologically ordered quantum many-body systems. They are neither bosons, nor fermions, and they can have a charge that is only a fraction of the elementary charge. Adiabatically exchanging anyons leads to nontrivial transformations of the quantum state that are robust if the anyons are well-separated throughout the process.
We have shown that one can use an optimized potential to shape and squeeze anyons [1]. This allows one to perform exchange operations within less space. We have also shown that anyons can be a helpful tool to detect phase transitions [2]. We have studied anyons in different types of lattice fractional quantum Hall models. In particular, we have found that quasielectrons can be constructed in a much simpler way in lattice models than in the continuum [3]. We have also shown that anyons can themselves form anyonic quasiparticles [4].
[1] PRResearch 3, 033044 (2021)
[2] PRResearch 2, 043443 (2020)
[3] NJP 20, 033029 (2018), PRB 99, 045147 (2019)
[4] PRB 102, 125117 (2020)
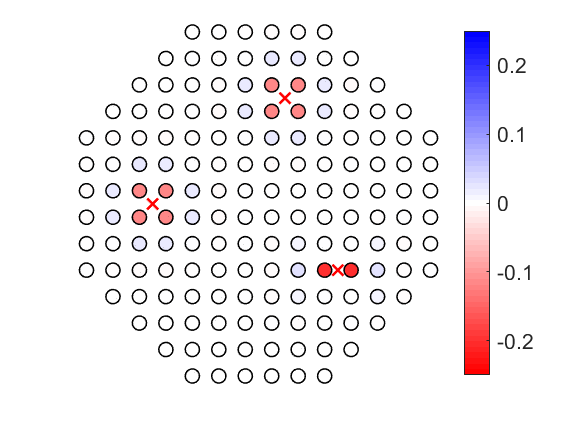
Fractional quantum Hall models on lattices
There is much interest in finding fractional quantum Hall models in lattice systems, such as the spin system shown on the right, because it may lead to new ways to realize fractional quantum Hall physics, and because the lattice gives rise to new effects and possibilities.
It has been found numerically that one can obtain fractional quantum Hall models in lattice systems by constructing a lattice Hamiltonian having many features in common with the Hamiltonian in the corresponding continuum systems. We have previously proposed a different route to obtain fractional quantum Hall models in lattice systems, in which one constructs lattice trial states and derive parent Hamiltonians for these states [1]. We have used this approach to construct various fractional quantum Hall models [2], including trial states for interfaces [3]. We have also investigated approaches to truncate the exact Hamiltonian to obtain simpler models with the same topology [4].
[1] PRL 108, 257206 (2012)
[2] PRB 94, 245104 (2016), PRB 98, 165147 (2018)
[3] PRB 101, 245164 (2020), PRB 103, 205149 (2021)
[4] Nat. Commun. 4, 2864 (2013), PRB 100, 035123 (2019)
Ultracold atoms in optical lattices
Ultracold atoms in optical lattices provide a versatile setup to investigate the physics of quantum many-body systems. We study dynamics of trapped ultracold atoms [1] and the possibility of implementing topological models in such systems [2].
[1] PRA 97, 013609 (2018)
[2] PRA 90, 013606 (2014)
