Dynamics of Quantum Information
Welcome to our group "Dynamics of quantum information"
Our group is interested in the dynamics of quantum many-body systems, with special attention paid to the role of quantum information and entanglement. The group’s research lies at the interface of condensed matter physics and quantum information, approaching the quantum many-body problem using a variety of theoretical and numerical approaches. Research topics include the dynamics of entanglement, quantum chaos and thermalization, unitary circuit models, and general aspects of non-equilibrium quantum dynamics.
Below you can find a selection of recent research conducted in this group.
Dual-unitary circuit dynamics
P. W. Claeys and A. Lamacraft
Dual-unitary quantum circuits can be used to construct 1+1 dimensional lattice models for which dynamical correlations of local observables can be explicitly calculated. We show how to analytically construct classes of dual-unitary circuits with any desired level of (non-)ergodicity for any dimension of the local Hilbert space, and present analytical results for thermalization to an infinite-temperature Gibbs state (ergodic) and a generalized Gibbs ensemble (nonergodic). It is shown how a tunable ergodicity-inducing perturbation can be added to a nonergodic circuit without breaking dual unitarity, leading to the appearance of prethermalization plateaux for local observables.
Phys. Rev. Lett. 126, 100603 (2021)
Selected as Editor’s Suggestion, Featured in Physics (Viewpoint) and for the cover of Physical Review Letters.
Transport in noisy spin chains
P. W. Claeys, A. Lamacraft, and J. Herzog-Arbeitman
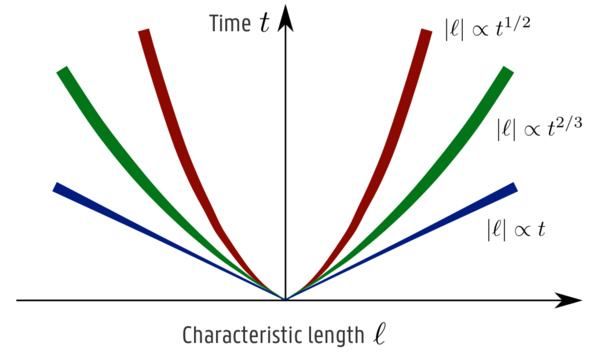
The dynamics of spin at finite temperature in the spin-1/2 Heisenberg chain was found to be superdiffusive in numerous recent numerical and experimental studies. Theoretical approaches to this problem have emphasized the role of nonabelian SU(2) symmetry as well as integrability, but the associated methods cannot be readily applied when integrability is broken. We examine spin transport in a spin-1/2 chain in which the exchange couplings fluctuate in space and time around a nonzero mean J, a model introduced by De Nardis et al. [Phys. Rev. Lett. 127, 057201 (2021)]. We show that operator dynamics in the strong noise limit at infinite temperature can be analyzed using conventional perturbation theory as an expansion in J. We find that regular diffusion persists at long times, albeit with an enhanced diffusion constant. The finite time spin dynamics is analyzed and compared with matrix product operator simulations.
Emergent quantum state designs
P. W. Claeys and A. Lamacraft
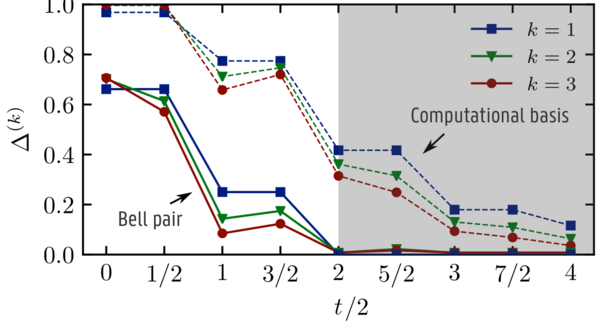
Recent works have investigated the emergence of a new kind of random matrix behaviour in unitary dynamics following a quantum quench. Starting from a time-evolved state, an ensemble of pure states supported on a small subsystem can be generated by performing projective measurements on the remainder of the system, leading to a projected ensembleprojected ensemble. In chaotic quantum systems it was conjectured that such projected ensembles become indistinguishable from the uniform Haar-random ensemble and lead to a quantum state designquantum state design. Exact results were recently presented by Ho and Choi [Phys. Rev. Lett. 128, 060601 (2022)] for the kicked Ising model at the self-dual point. We provide an alternative construction that can be extended to general chaotic dual-unitary circuits with solvable initial states and measurements, highlighting the role of the underlying dual-unitarity and further showing how dual-unitary circuit models exhibit both exact solvability and random matrix behaviour. Building on results from biunitary connections, we show how complex Hadamard matrices and unitary error bases both lead to solvable measurement schemes.