Computational Quantum Many-Body Physics

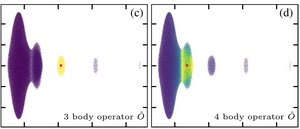
To characterize the generic behavior of open quantum systems, we consider random, purely dissipative Liouvillians with a notion of locality. We find that the positivity of the map implies a sharp separation of the relaxation timescales according to the locality of observables. Specifically, we analyze a spin-1/2 system of size ? with up to n-body Lindblad operators, which are n local in the complexity-theory sense. Without locality (n=l), the complex Liouvillian spectrum densely covers a “lemon”-shaped support, in agreement with recent findings [S. Denisov et al., Phys. Rev. Lett. 123, 140403 (2019)]. However, for local Liouvillians (n<l), we find that the spectrum is composed of several dense clusters with random matrix spacing statistics, each featuring a lemon-shaped support wherein all eigenvectors correspond to n-body decay modes. This implies a hierarchy of relaxation timescales of n-body observables, which we verify to be robust in the thermodynamic limit. Our findings for n locality generalize immediately to the case of spatial locality, introducing further splitting of timescales due to the additional structure.

Phys. Rev. Lett.124, 100604 (2020)

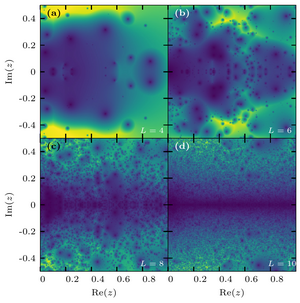
We show that in a generic, ergodic quantum many-body system the interactions induce a nontrivial topology for an arbitrarily small non-Hermitian component of the Hamiltonian. This is due to an exponential-in-system-size proliferation of exceptional points which have the Hermitian limit as an accumulation (hyper)surface. The nearest-neighbor level repulsion characterizing Hermitian ergodic many-body systems is thus shown to be a projection of a richer phenomenology, where actually all the exponentially many eigenvalues are pairwise connected in a topologically robust fashion via exceptional points.

Phys. Rev. Research, 1, 033051 (2019)

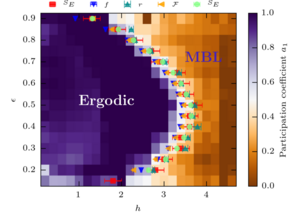
We present a large-scale exact diagonalization study of the one-dimensional spin-1/2 Heisenberg model in a random magnetic field. In order to access properties at varying energy densities across the entire spectrum for system sizes up to L=22 spins, we use a spectral transformation which can be applied in a massively parallel fashion. Our results allow for an energy-resolved interpretation of the many-body localization transition including the existence of an extensive many-body mobility edge. The ergodic phase is well characterized by Gaussian orthogonal ensemble statistics, volume-law entanglement, and a full delocalization in the Hilbert space. Conversely, the localized regime displays Poisson statistics, area-law entanglement, and nonergodicity in the Hilbert space where a true localization never occurs. We perform finite-size scaling to extract the critical edge and exponent of the localization length divergence.

Phys. Rev. B 91, 081103(R) (2015)

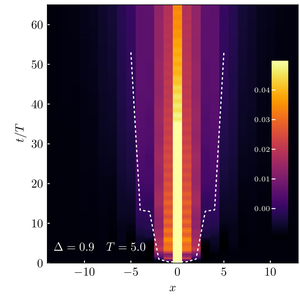
Using a numerically exact method we study the stability of dynamical localization to the addition of interactions in a periodically driven isolated quantum system which conserves only the total number of particles. We find that while even infinitesimally small interactions destroy dynamical localization, for weak interactions density transport is significantly suppressed and is asymptotically diffusive, with a diffusion coefficient proportional to the interaction strength. For systems tuned away from the dynamical localization point, even slightly, transport is dramatically enhanced and within the largest accessible systems sizes a diffusive regime is only pronounced for sufficiently small detunings.

SciPost Phys.3, 029 (2017)

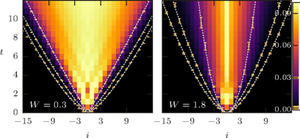
Entanglement growth and out-of-time-order correlators (OTOC) are used to assess the propagation of information in isolated quantum systems. In this work, using large scale exact time evolution we show that for weakly disordered nonintegrable systems information propagates behind a ballistically moving front, and the entanglement entropy growths linearly in time. For stronger disorder the motion of the information front is algebraic and subballistic and is characterized by an exponent, which depends on the strength of the disorder, similarly to the sublinear growth of the entanglement entropy. We show that the dynamical exponent associated with the information front coincides with the exponent of the growth of the entanglement entropy for both weak and strong disorder. We also demonstrate that the temporal dependence of the OTOC is characterized by a fast nonexponential growth, followed by a slow saturation after the passage of the information front. Finally, we discuss the implications of this behavioral change on the growth of the entanglement entropy.

Phys. Rev. B96, 020406(R) (2017)

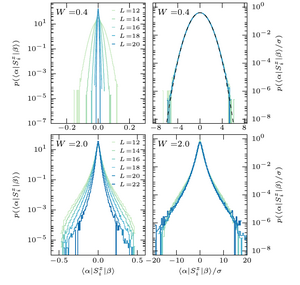
It is commonly believed that quantum isolated systems satisfying the eigenstate thermalization hypothesis (ETH) are diffusive. We show that this assumption is too restrictive since there are systems that are asymptotically in a thermal state yet exhibit anomalous, subdiffusive thermalization. We show that such systems satisfy a modified version of the ETH ansatz and derive a general connection between the scaling of the variance of the off-diagonal matrix elements of local operators, written in the eigenbasis of the Hamiltonian, and the dynamical exponent. We find that for subdiffusively thermalizing systems the variance scales more slowly with system size than expected for diffusive systems. We corroborate our findings by numerically studying the distribution of the coefficients of the eigenfunctions and the off-diagonal matrix elements of local operators of the random field Heisenberg chain, which has anomalous transport in its thermal phase. Surprisingly, this system also has non-Gaussian distributions of the eigenfunctions, thus, directly violating Berry’s conjecture.

Phys. Rev. Lett. 117, 170404 (2016)