Many-body localized phases may not only be characterized by their ergodicity breaking, but
can also host ordered phases such as the many-body localized spin-glass (MBL-SG). The MBL-
SG is challenging to access in a dynamical measurement and therefore experimentally since
the conventionally used Edwards-Anderson order parameter is a two-point correlation function
in time. In this work, we show that many-body localized spin-glass order can also be detected
from two-site reduced density matrices, which we use to construct an eigenstate spin-glass order
parameter. We find that this eigenstate spin-glass order parameter captures spin-glass phases in
random Ising chains both in many-body eigenstates as well as in the nonequilibrium dynamics
from a local in time measurement. We discuss how our results can be used to observe MBL-SG
order within current experiments in Rydberg atoms and trapped ion systems.
Phys. Rev. B 99, 144201 (2019)
Eigenstate order
Eigenstate order
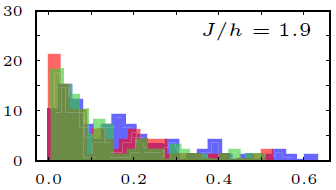
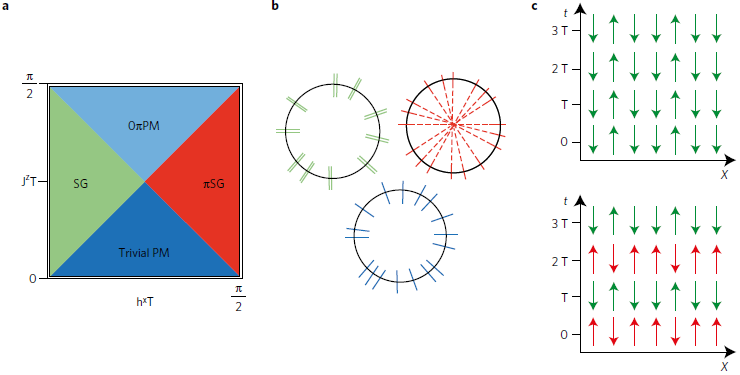
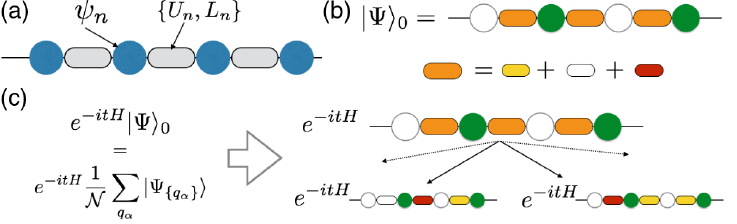
Phases of quantum many-body systems are conventionally described in terms of their thermodynamic properties. Recent developments suggest that it is suitable in a more general context to extend the characterization of quantum many-body systems beyond this thermodynamic equilibrium paradigm to the level of single eigenstates. The associated eigenstate phases are protected by nonergodicity where systems fail to approach thermodynamic states under their dynamics. This opens up the possibility for new kinds of order in quantum real-time evolution, although respective thermodynamic states are completely featureless. A prominent example in this direction has become the so-called $\pi$-spin glass phase also named discrete time crystal, which has been discovered at our institute. Contrary to conventional phases these time crystals display not only spatial but rather spatio-temporal order with a time-dependent order parameter.
In the condensed matter division of our institute we study the mechanisms for the underlying ergodicity breaking, explore the possibilities for new dynamical eigenstate phases, and develop techniques for the challenging theoretical description of such nonequilibrium systems. For more details on current and recent research highlights see the collection below.
Equilibration and order in quantum Floquet matter
R. Moessner, S. L. Sondhi
Equilibrium thermodynamics is characterized by two fundamental ideas: thermalization-that
systems approach a late time thermal state; and phase structure-that thermal states exhibit
singular changes as various parameters characterizing the system are changed. We summarize
recent progress that has established generalizations of these ideas to periodically driven, or
Floquet, closed quantum systems. This has resulted in the discovery of entirely new phases which
exist only out of equilibrium, such as the π-spin glass/Floquet time crystal.
Nature Physics 13, 424 (2017)
Nature Physics 13, 424 (2017)
Many-Body Localization Dynamics from Gauge Invariance
Marlon Brenes, Marcello Dalmonte, Markus Heyl, Antonello
Scardicchio
We show how lattice gauge theories can display many-body localization dynamics in the absence
of disorder. Our starting point is the observation that, for some generic translationally invariant
states, the Gauss law effectively induces a dynamics which can be described as a disorder
average over gauge superselection sectors. We carry out extensive exact simulations on the real-
time dynamics of a lattice Schwinger model, describing the coupling between U(1) gauge fields
and staggered fermions. Our results show how memory effects and slow, double-logarithmic
entanglement growth are present in a broad regime of parameters-in particular, for sufficiently
large interactions. These findings are immediately relevant to cold atoms and trapped ion
experiments realizing dynamical gauge fields and suggest a new and universal link between
confinement and entanglement dynamics in the many-body localized phase of lattice models.
Phys. Rev. Lett. 120, 030601 (2018)
Phys. Rev. Lett. 120, 030601 (2018)