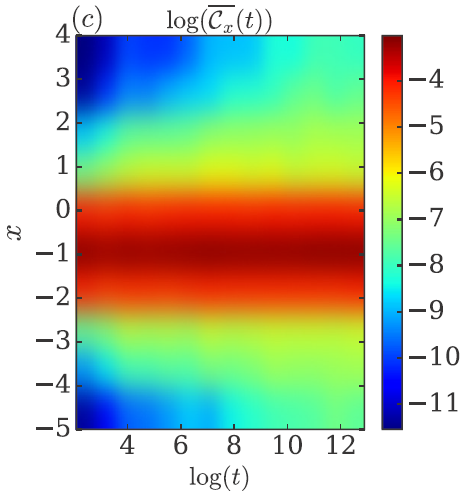
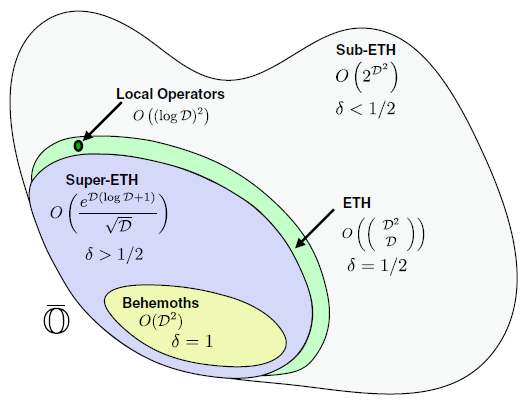
Many-body localization

Many-body localization

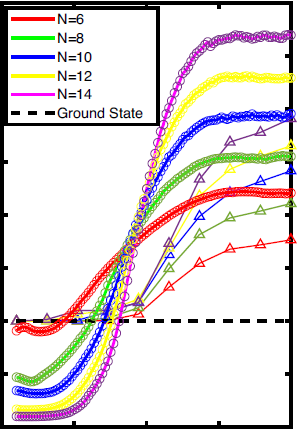
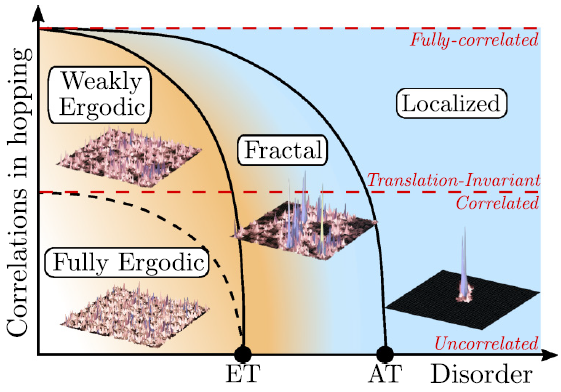
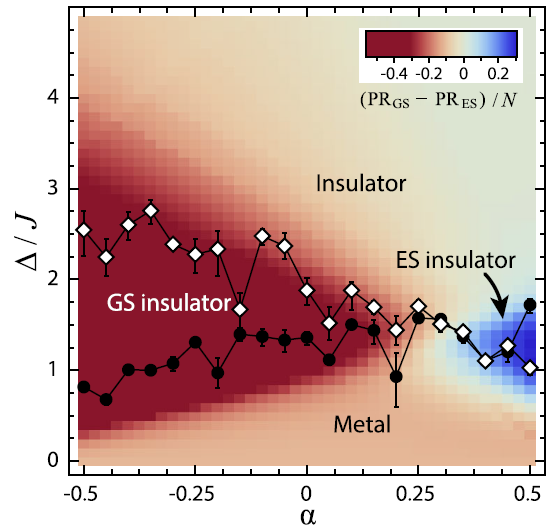
Generic interacting quantum systems show a remarkable universal dynamical behavior: Largely independently of details of initial conditions, these systems unavoidably approach the thermodynamic equilibrium in the course of time. Therefore, it came as a big surprise that in the presence of strong disorder this thermalization process can fail due to localization, preventing efficient energy exchange across the microscopic degrees of freedom. This led to the discovery of a new dynamical phase of matter of many-body localized particles. The physics shares similarities to localization of noninteracting particles in a strong disorder potential, known as Anderson localization. However, interaction effects beyond the single-particle limit turn out to be crucial.

As a consequence of the broken ergodicity many-body localized phases go beyond the thermodynamic paradigm and allow for novel kinds of phases and order. Due to its interacting nature, the many-body localized phase and specifically also the transition towards ergodicity are challenging to address theoretically.

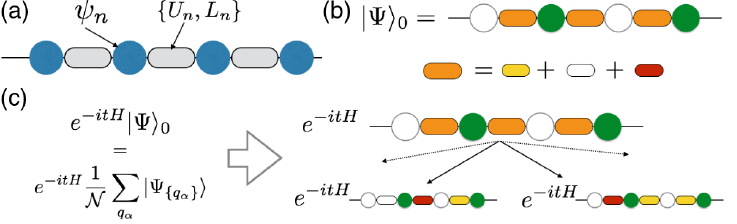
We develop both analytical as well as high performance numerical methods to study and characterize many-body localized phases and the new kinds of order that can appear in such systems. For more details on current and recent research highlights see the collection below.


Many-body Delocalization via Emergent Symmetry
N. S. Srivatsa, R. Moessner, and A. E. B. Nielsen

Many-body localization (MBL) provides a mechanism to avoid thermalization in many-body quantum systems. Here, we show that an emergent symmetry can protect a state from MBL. Specifically, we propose a Z2 symmetric model with nonlocal interactions, which has an analytically known, SU(2) invariant, critical ground state. At large disorder strength, all states at finite energy density are in a glassy MBL phase, while the lowest energy states are not. These do, however, localize when a perturbation destroys the emergent SU(2) symmetry. The model also provides an example of MBL in the presence of nonlocal, disordered interactions that are more structured than a power law. Finally, we show how the protected state can be moved into the bulk of the spectrum.

Phys. Rev. Lett. 125, 240401 (2020)




Correlation-induced localization
P. A. Nosov, I. M. Khaymovich, and V. E. Kravtsov

A new paradigm of Anderson localization caused by correlations in the long-range hopping along with uncorrelated on-site disorder is considered which requires a more precise formulation of the basic localization-delocalization principles. A new class of random Hamiltonians with translation- invariant hopping integrals is suggested and the localization properties of such models are established both in the coordinate and in the momentum spaces alongside with the corresponding level statistics. Duality of translation-invariant models in the momentum and coordinate space is uncovered and exploited to find a full localization-delocalization phase diagram for such models. The crucial role of the spectral properties of hopping matrix is established and a new matrix inversion trick is suggested to generate a one-parameter family of equivalent localization- delocalization problems. Optimization over the free parameter in such a transformation together with the localization-delocalization principles allows us to establish exact bounds for the localized and ergodic states in long-range hopping models. When applied to the random matrix models with deterministic power-law hopping this transformation allows to confirm localization of states at all values of the exponent in power-law hopping and to prove analytically the symmetry of the exponent in the power-law localized wave functions.

Phys. Rev. B 99, 104203 (2019)




Many-Body Localization Dynamics from Gauge Invariance
Marlon Brenes, Marcello Dalmonte, Markus Heyl, Antonello Scardicchio

We show how lattice gauge theories can display many-body localization dynamics in the absence of disorder. Our starting point is the observation that, for some generic translationally invariant states, the Gauss law effectively induces a dynamics which can be described as a disorder average over gauge superselection sectors. We carry out extensive exact simulations on the real- time dynamics of a lattice Schwinger model, describing the coupling between U(1) gauge fields and staggered fermions. Our results show how memory effects and slow, double-logarithmic entanglement growth are present in a broad regime of parameters-in particular, for sufficiently large interactions. These findings are immediately relevant to cold atoms and trapped ion experiments realizing dynamical gauge fields and suggest a new and universal link between confinement and entanglement dynamics in the many-body localized phase of lattice models.

Phys. Rev. Lett. 120, 030601 (2018)





Interactions and Mobility Edges: Observing the Generalized Aubry-André Model
F. A. An, K. Padavić, E. J. Meier, S. Hegde, S. Ganeshan, J. H. Pixley, S. Vishveshwara, and B. Gadway

Using synthetic lattices of laser-coupled atomic momentum modes, we experimentally realize a recently proposed family of nearest-neighbor tight-binding models having quasiperiodic site energy modulation that host an exact mobility edge protected by a duality symmetry. These one- dimensional tight-binding models can be viewed as a generalization of the well-known Aubry- André model, with an energy-dependent selfduality condition that constitutes an analytical mobility edge relation. By adiabatically preparing low and high energy eigenstates of this model system and performing microscopic measurements of their participation ratio, we track the evolution of the mobility edge as the energy-dependent density of states is modified by the model’s tuning parameter. Our results show strong deviations from single-particle predictions, consistent with attractive interactions causing both enhanced localization of the lowest energy state due to self-trapping and inhibited localization of high energy states due to screening. This study paves the way for quantitative studies of interaction effects on self-duality induced mobility edges.

Phys. Rev. Lett. 126, 040603 (2020)




Fragile extended phases in the log-normal Rosenzweig-Porter model
I. M. Khaymovich, V. E. Kravtsov, B. L. Altshuler, and L. B. Ioffe

In this paper, we suggest an extension of the Rosenzweig-Porter (RP) model, the LN-RP model, in which the off-diagonal matrix elements have a wide, log-normal distribution. We argue that this model is more suitable to describe a generic many-body localization problem. In contrast to RP model, in LN-RP model, a fragile weakly ergodic phase appears that is characterized by broken basis-rotation symmetry which the fully ergodic phase, also present in this model, strictly respects in the thermodynamic limit. Therefore, in addition to the localization and ergodic transitions in LN-RP model, there exists also the transition between the two ergodic phases (FWE transition). We suggest new criteria of stability of the nonergodic phases that give the points of localization and ergodic transitions and prove that the Anderson localization transition in LN-RP model involves a jump in the fractal dimension of the egenfunction support set. We also formulate the criterion of FWE transition and obtain the full phase diagram of the model. We show that truncation of the log-normal tail shrinks the region of weakly ergodic phase and restores the multifractal and the fully ergodic phases.

Phys. Rev. Research 2, 043346 (2020)




Efficiently solving the dynamics of many-body localized systems at strong disorder
Giuseppe De Tomasi, Frank Pollmann, Markus Heyl

We introduce a method to efficiently study the dynamical properties of many-body localized systems in the regime of strong disorder and weak interactions. Our method reproduces qualitatively and quantitatively the time evolution with a polynomial effort in system size and independent of the desired time scales. We use our method to study quantum information propagation, correlation functions, and temporal fluctuations in one- and two-dimensional many- body localization systems. Moreover, we outline strategies for a further systematic improvement of the accuracy and we point out relations of our method to recent attempts to simulate the time dynamics of quantum many-body systems in classical or artificial neural networks.

Phys. Rev. B 99, 241114 (2019)



❮❯


Multifractality Meets Entanglement: Relation for Nonergodic Extended States
Giuseppe De Tomasi and Ivan M. Khaymovich

In this work, we establish a relation between entanglement entropy and fractal dimension D of generic many-body wave functions, by generalizing the result of Page [Phys. Rev. Lett. 71, 1291 (1993)] to the case of sparse random pure states (SRPS). These SRPS living in a Hilbert space of size N are defined as normalized vectors with only N D (0 ≤ D ≤ 1) random nonzero elements. For D = 1, these states used by Page represent ergodic states at an infinite temperature. However, for 0 < D < 1, the SRPS are nonergodic and fractal, as they are confined in a vanishing ratio N D / N of the full Hilbert space. Both analytically and numerically, we show that the mean entanglement entropy S1(A) of a subsystem A, with Hilbert space dimension NA, scales as S̅1(A) ∼ D ln N for small fractal dimensions D, ND < NA. Remarkably, S̅1(A) saturates at its thermal (Page) value at an infinite temperature, S̅1(A) ∼ ln NA at larger D. Consequently, we provide an example when the entanglement entropy takes an ergodic value even though the wave function is highly nonergodic. Finally, we generalize our results to Renyi entropies Sq (A) with q > 1 and to genuine multifractal states and also show that their fluctuations have ergodic behavior in a narrower vicinity of the ergodic state D = 1.

Phys. Rev. Lett. 124, 200602 (2020)




Eigenstate Thermalization, Random Matrix Theory, and Behemoths
Ivan M. Khaymovich, Masudul Haque, and Paul A. McClarty

The eigenstate thermalization hypothesis (ETH) is one of the cornerstones of contemporary quantum statistical mechanics. The extent to which ETH holds for nonlocal operators is an open question that we partially address in this Letter. We report on the construction of highly nonlocal operators, behemoths, that are building blocks for various kinds of local and nonlocal operators. The behemoths have a singular distribution and width w ∼ D -1 (D being the Hilbert space dimension). From there, one may construct local operators with the ordinary Gaussian distribution and w ∼ D -1/2 in agreement with ETH. Extrapolation to even larger widths predicts sub-ETH behavior of typical nonlocal operators with w ∼ D -δ, 0 < δ < 1/2. This operator construction is based on a deep analogy with random matrix theory and shows striking agreement with numerical simulations of nonintegrable many-body systems.

Phys. Rev. Lett. 122, 070601 (2019)



❮❯