The efficient numerical simulation of nonequilibrium real-time evolution in isolated quantum
matter constitutes a key challenge for current computational methods. This holds in particular
in the regime of two spatial dimensions, whose experimental exploration is currently pursued
with strong efforts in quantum simulators. In this work we present a versatile and efficient
machine learning inspired approach based on a recently introduced artificial neural network
encoding of quantum many-body wave functions. We identify and resolve key challenges for the
simulation of time evolution, which previously imposed significant limitations on the accurate
description of large systems and long-time dynamics. As a concrete example, we study the
dynamics of the paradigmatic two-dimensional transverse-field Ising model, as recently also
realized experimentally in systems of Rydberg atoms. Calculating the nonequilibrium real-time
evolution across a broad range of parameters, we, for instance, observe collapse and revival
oscillations of ferromagnetic order and demonstrate that the reached timescales are comparable
to or exceed the capabilities of state-of-the-art tensor network methods.
Phys. Rev. Lett. 125, 100503 (2020)
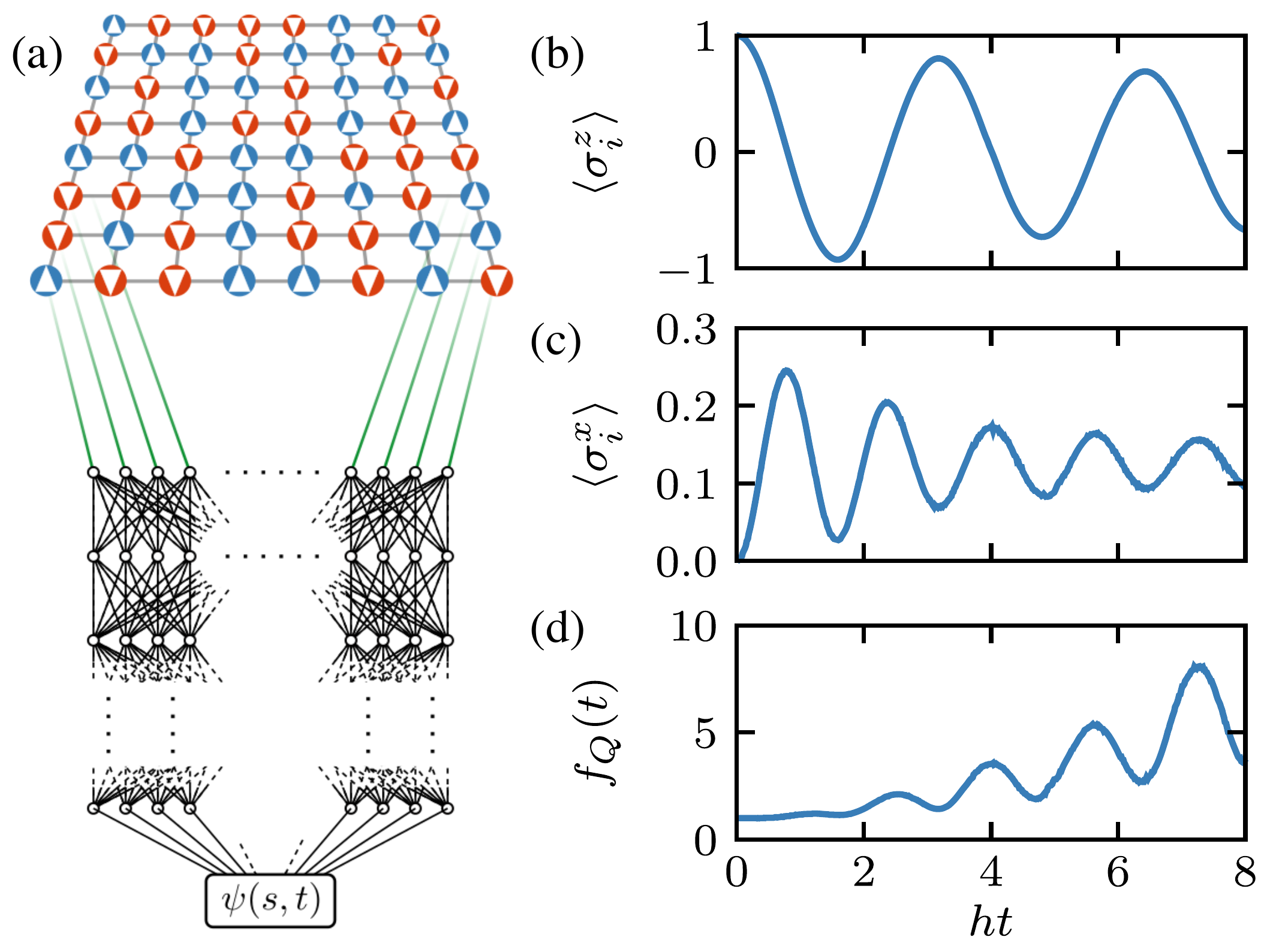
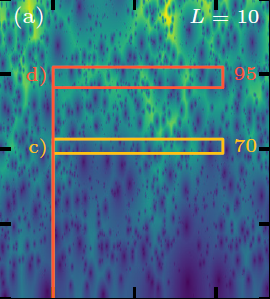
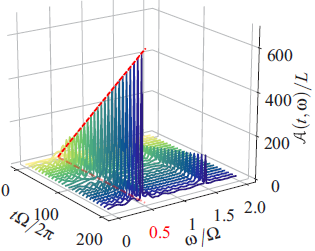
Nonequilibrium phases and phase transitions
Nonequilibrium phases and phase transitions
Recent experimental progress has brought into existence so-called quantum simulators such as ultracold atoms in optical lattices or trapped ions. These act like an 'analogue' quantum computer by mimicking the behaviour of quantum systems whose properties we are interested in.
In particular, these quantum simulators can be used to study in a controlled way the nonequilibrium dynamics of closed quantum many-body systems. For such nonequilibrium quantum states, the thermodynamic concept of a free energy is not applicable. On the one hand this implies the absence of organizing principles such as the minimization of free energies making a systematic understanding of such states challenging. On the other hand these states promise to show new properties not constrained by the principles of equilibrium thermodynamics.
A natural question is to which extent there are phases of matter without the existence of a free energy? Can these systems exhibit universal behavior independent of microscopic details similar to what happens at equilibrium continuous phase transitions?
We address such questions and develop concepts that allow for a systematic understanding not only for individual problems, but rather for classes of phenomena. This includes the theory of dynamical quantum phase transitions or the construction of dynamical potentials for eigenstate phases. For more details on current and recent research highlights see the collection below.
Odd elasticity
C. Scheibner, A. Souslov, D. Banerjee, P. Surówka, W. T. M. Irvine,
V. Vitelli
A passive solid cannot do work on its surroundings through any quasistatic cycle of deformations.
This property places strong constraints on the allowed elastic moduli. In this Article, we show
that static elastic moduli altogether absent in passive elasticity can arise from active, non-
conservative microscopic interactions. These active moduli enter the antisymmetric (or odd)
part of the static elastic modulus tensor and quantify the amount of work extracted along
quasistatic strain cycles. In two-dimensional isotropic media, two chiral odd-elastic moduli
emerge in addition to the bulk and shear moduli. We discuss microscopic realizations that include
networks of Hookean springs augmented with active transverse forces and non-reciprocal active
hinges. Using coarse-grained microscopic models, numerical simulations and continuum equations,
we uncover phenomena ranging from auxetic behaviour induced by odd moduli to elastic wave
propagation in overdamped media enabled by self-sustained active strain cycles. Our work sheds
light on the non-Hermitian mechanics of two- and three-dimensional active solids that conserve
linear momentum but exhibit a non-reciprocal linear response.
Nature Physics 16, 475 (2020)
Nature Physics 16, 475 (2020)
Quantum paracrystalline shear modes of the electron liquid
J. Y. Khoo, P.-Y. Chang, F. Pientka, I. Sodemann
Unlike classical fluids, a quantum Fermi liquid can support a long-lived and propagating shear
sound wave at arbitrarily small wave vectors and frequencies, reminiscent of the transverse sound
in crystals, despite lacking any form of long-range crystalline order. This mode is expected to be
present in moderately interacting metals where the quasiparticle mass is renormalized to be more
than twice the bare mass in two dimensions (2D), but it has remained undetected because it is
hard to excite since it does not involve charge density fluctuations, in contrast to the conventional
plasma mode. In this work we propose a strategy to excite and detect this unconventional mode
in clean metallic channels. We show that the shear sound is responsible for the appearance
of sharp dips in the ac conductance of narrow channels at resonant frequencies matching its
dispersion. The liquid resonates while minimizing its dissipation in an analogous fashion to a
sliding crystal. Ultraclean 2D materials that can be tuned toward the Wigner crystallization
transition such as silicon metal-oxide-semiconductor field-effect transistors, MgZnO/ZnO, p-
GaAs, and AlAs quantum wells are promising platforms to experimentally discover the shear
sound.
Phys. Rev. B 102, 085437 (2020)
Phys. Rev. B 102, 085437 (2020)
