Dynamics in Correlated Quantum Matter
Dynamics in correlated quantum matter
In our research we are interested in the dynamics of correlated quantum matter at the interface between quantum many-body theory, nonequilibrium physics, quantum information science, and machine learning.
The research covers the development of a theory of dynamical quantum phase transitions, extending the concept of phase transitions to the time domain, the dynamics in lattice gauge theories, the exploration of machine learning techniques as a new toolbox in quantum many-body theory, many-body localization in interacting strongly disordered systems, or entanglement in correlated quantum matter.
Below you can find a selection of recent research conducted in this group.
Reinforcement Learning for Digital Quantum Simulation
A. Bolens and M. Heyl
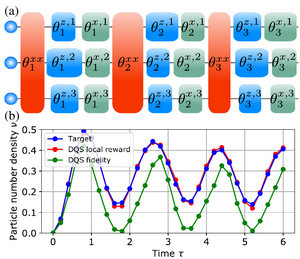
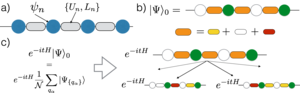
Digital quantum simulation on quantum computers provides the potential to simulate the unitary evolution of any many-body Hamiltonian with bounded spectrum by discretizing the time evolution operator through a sequence of elementary quantum gates. A fundamental challenge in this context originates from experimental imperfections, which critically limits the number of attainable gates within a reasonable accuracy and therefore the achievable system sizes and simulation times. In this work, we introduce a reinforcement learning algorithm to systematically build optimized quantum circuits for digital quantum simulation upon imposing a strong constraint on the number of quantum gates. With this we consistently obtain quantum circuits that reproduce physical observables with as little as three entangling gates for long times and large system sizes up to 16 qubits. As concrete examples we apply our formalism to a long-range Ising chain and the lattice Schwinger model. Our method demonstrates that digital quantum simulation on noisy intermediate scale quantum devices can be pushed to much larger scale within the current experimental technology by a suitable engineering of quantum circuits using reinforcement learning.
Phys. Rev. Lett. 127, 110502 (2021)
Unitary Long-Time Evolution with Quantum Renormalization Groups and Artificial Neural Networks
H. Burau and M. Heyl
In this work, we combine quantum renormalization group approaches with deep artificial neural networks for the description of the real-time evolution in strongly disordered quantum matter. We find that this allows us to accurately compute the long-time coherent dynamics of large many-body localized systems in nonperturbative regimes including the effects of many-body resonances. Concretely, we use this approach to describe the spatiotemporal buildup of many-body localized spin-glass order in random Ising chains. We observe a fundamental difference to a noninteracting Anderson insulating Ising chain, where the order only develops over a finite spatial range. We further apply the approach to strongly disordered two-dimensional Ising models, highlighting that our method can be used also for the description of the real-time dynamics of nonergodic quantum matter in a general context.
Phys. Rev. Lett. 127, 050601 (2021).
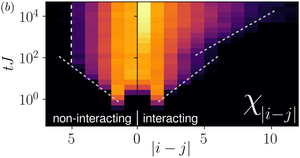
Disorder-Free Localization in an Interacting 2D Lattice Gauge Theory
P. Karpov, R. Verdel, Y.-P. Huang, M. Schmitt, and M. Heyl
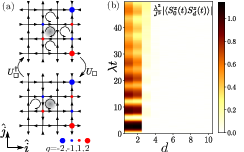
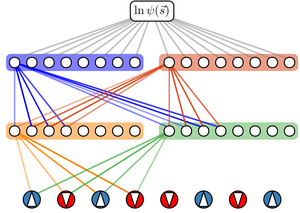
Disorder-free localization has been recently introduced as a mechanism for ergodicity breaking in low-dimensional homogeneous lattice gauge theories caused by local constraints imposed by gauge invariance. We show that also genuinely interacting systems in two spatial dimensions can become nonergodic as a consequence of this mechanism. This result is all the more surprising since the conventional many-body localization is conjectured to be unstable in two dimensions; hence the gauge invariance represents an alternative robust localization mechanism surviving in higher dimensions in the presence of interactions. Specifically, we demonstrate nonergodic behavior in the quantum link model by obtaining a bound on the localization-delocalization transition through a classical correlated percolation problem implying a fragmentation of Hilbert space on the nonergodic side of the transition. We study the quantum dynamics in this system by introducing the method of “variational classical networks,” an efficient and perturbatively controlled representation of the wave function in terms of a network of classical spins akin to artificial neural networks. We identify a distinguishing dynamical signature by studying the propagation of line defects, yielding different light cone structures in the localized and ergodic phases, respectively. The methods we introduce in this work can be applied to any lattice gauge theory with finite-dimensional local Hilbert spaces irrespective of spatial dimensionality.
Phys. Rev. Lett. 126, 130401 (2021)
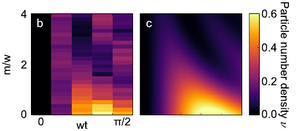
Quantum Many-Body Dynamics in Two Dimensions with Artificial Neural Networks
M. Schmitt and M. Heyl
The efficient numerical simulation of nonequilibrium real-time evolution in isolated quantum matter constitutes a key challenge for current computational methods. This holds in particular in the regime of two spatial dimensions, whose experimental exploration is currently pursued with strong efforts in quantum simulators. In this work we present a versatile and efficient machine learning inspired approach based on a recently introduced artificial neural network encoding of quantum many-body wave functions. We identify and resolve some key challenges for the simulation of time evolution, which previously imposed significant limitations on the accurate description of large systems and long-time dynamics. As a concrete example, we study the dynamics of the paradigmatic two-dimensional transverse field Ising model, as recently also realized experimentally in systems of Rydberg atoms. Calculating the nonequilibrium real-time evolution across a broad range of parameters, we, for instance, observe collapse and revival oscillations of ferromagnetic order and demonstrate that the reached time scales are comparable to or exceed the capabilities of state-of-the-art tensor network methods.
Phys. Rev. Lett. 125, 100503 (2020)
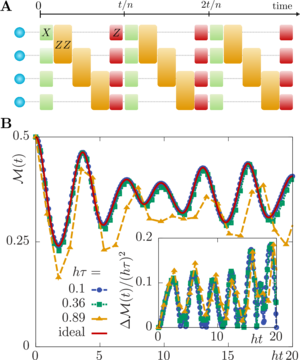
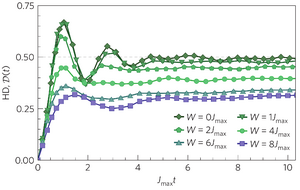
Quantum localization bounds Trotter errors in digital quantum simulation
M. Heyl, P. Hauke, P. Zoller
A fundamental challenge in digital quantum simulation (DQS) is the control of an inherent error, which appears when discretizing the time evolution of a quantum many-body system as a sequence of quantum gates, called Trotterization. Here, we show that quantum localization-by constraining the time evolution through quantum interference-strongly bounds these errors for local observables, leading to an error independent of system size and simulation time. DQS is thus intrinsically much more robust than suggested by known error bounds on the global many-body wave function. This robustness is characterized by a sharp threshold as a function of the Trotter step size, which separates a localized region with controllable Trotter errors from a quantum chaotic regime. Our findings show that DQS with comparatively large Trotter steps can retain controlled errors for local observables. It is thus possible to reduce the number of gate operations required to represent the desired time evolution faithfully.
Science Adv. 5, eaau8342 (2019)
Many-Body Localization Dynamics from Gauge Invariance
M. Brenes, M. Dalmonte, M. Heyl, and A. Scardicchio
We show how lattice gauge theories can display many-body localization dynamics in the absence of disorder. Our starting point is the observation that, for some generic translationally invariant states, the Gauss law effectively induces a dynamics which can be described as a disorder average over gauge superselection sectors. We carry out extensive exact simulations on the real-time dynamics of a lattice Schwinger model, describing the coupling between U(1) gauge fields and staggered fermions. Our results show how memory effects and slow, double-logarithmic entanglement growth are present in a broad regime of parameters—in particular, for sufficiently large interactions. These findings are immediately relevant to cold atoms and trapped ion experiments realizing dynamical gauge fields and suggest a new and universal link between confinement and entanglement dynamics in the many-body localized phase of lattice models.
Phys. Rev. Lett. 120, 030601 (2018)
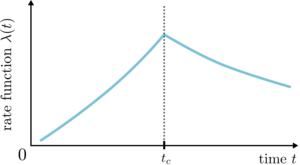
Dynamical quantum phase transitions: a review
M. Heyl
Quantum theory provides an extensive framework for the description of the equilibrium properties of quantum matter. Yet experiments in quantum simulators have now opened up a route towards the generation of quantum states beyond this equilibrium paradigm. While these states promise to show properties not constrained by equilibrium principles, such as the equal a priori probability of the microcanonical ensemble, identifying the general properties of nonequilibrium quantum dynamics remains a major challenge, especially in view of the lack of conventional concepts such as free energies. The theory of dynamical quantum phase transitions attempts to identify such general principles by lifting the concept of phase transitions to coherent quantum real-time evolution. This review provides a pedagogical introduction to this field. Starting from the general setting of nonequilibrium dynamics in closed quantum many-body systems, we give the definition of dynamical quantum phase transitions as phase transitions in time with physical quantities becoming nonanalytic at critical times. We summarize the achieved theoretical advances as well as the first experimental observations, and furthermore provide an outlook to major open questions as well as future directions of research.
Rep. Prog. Phys. 81, 054001 (2018)
Real-time dynamics of lattice gauge theories with a few-qubit quantum computer
E. A. Martinez, C. A. Muschik, P. Schindler, D. Nigg, A. Erhard, M. Heyl, P. Hauke, M. Dalmonte, T. Monz, P. Zoller, and R. Blatt
Gauge theories are fundamental to our understanding of interactions between the elementary constituents of matter as mediated by gauge bosons. However, computing the real-time dynamics in gauge theories is a notorious challenge for classical computational methods. In the spirit of Feynman's vision of a quantum simulator, this has recently stimulated theoretical effort to devise schemes for simulating such theories on engineered quantum-mechanical devices, with the difficulty that gauge invariance and the associated local conservation laws (Gauss laws) need to be implemented. Here we report the first experimental demonstration of a digital quantum simulation of a lattice gauge theory, by realising 1+1-dimensional quantum electrodynamics (Schwinger model) on a few-qubit trapped-ion quantum computer. We are interested in the real-time evolution of the Schwinger mechanism, describing the instability of the bare vacuum due to quantum fluctuations, which manifests itself in the spontaneous creation of electron-positron pairs. To make efficient use of our quantum resources, we map the original problem to a spin model by eliminating the gauge fields in favour of exotic long-range interactions, which have a direct and efficient implementation on an ion trap architecture. We explore the Schwinger mechanism of particle-antiparticle generation by monitoring the mass production and the vacuum persistence amplitude. Moreover, we track the real-time evolution of entanglement in the system, which illustrates how particle creation and entanglement generation are directly related. Our work represents a first step towards quantum simulating high-energy theories with atomic physics experiments, the long-term vision being the extension to real-time quantum simulations of non-Abelian lattice gauge theories.
Nature 534, 516 (2016)
Many-body localization in a quantum simulator with programmable random disorder
J. Smith, A. Lee, P. Richerme, B. Neyenhuis, P. W. Hess, P. Hauke, M. Heyl, D. A. Huse, and C. Monroe
When a system thermalizes it loses all memory of its initial conditions. Even within a closed quantum system, subsystems usually thermalize using the rest of the system as a heat bath. Exceptions to quantum thermalization have been observed, but typically require inherent symmetries or noninteracting particles in the presence of static disorder. However, for strong interactions and high excitation energy there are cases, known as many-body localization (MBL), where disordered quantum systems can fail to thermalize. We experimentally generate MBL states by applying an Ising Hamiltonian with long-range interactions and programmable random disorder to ten spins initialized far from equilibrium. Using experimental and numerical methods we observe the essential signatures of MBL: initial-state memory retention, Poissonian distributed energy level spacings, and evidence of long-time entanglement growth. Our platform can be scaled to more spins, where a detailed modelling of MBL becomes impossible.
Nature Phys. 12, 907 (2016)