Frank Jülicher
Frank Jülicher
Max-Planck-Institute
for the Physics of Complex Systems
Nöthnitzer Straße 38
01187 Dresden
Germany
Tel. +49 351 871-1202
Fax. +49 351 871-1299
e-Mail: julicher@pks.mpg.de

Research Interests
Theory of Biological Systems and Processes
The main focus of our research is to develop theoretical approaches to understand living matter at the scale of cells and tissues. Work on active cellular processes includes the study of active chemical processes, cellular signaling and the cytoskeletal dynamics during cell division, cellular force generation and cell motility. Biological condensates provide membraneless compartments in the cell that can be understood as coexisting phases or phase separated droplets. Finally, we investigate the biophysical properties and dynamics of tissues and epithelia. Based on the properties of individual cells and of cellular signaling systems, we are interested in the dynamics of developmental processes, for example wing development in the fruit fly and the self-organization of organoids.
Research topics include:
Active cellular processes
Active droplet physics
Cellular oscillations
Cell electrohydraulics
Swimming of microorganisms
Cell locomotion
Physics of the cytoskeleton and of motor proteins
Active gels and fluids
Collective behaviors of motor proteins
Self-organization phenomena in the cytoskeleton
Physics of Cell Division
Asymmetric dell division
Physics of the mitotic spindle
Control of growth and division
Tissues and developmental processes
Cellular packings in epithelia
Cellular rearrangements during growth and development
Morphogen signaling and morphogen gradient formation
Biophysics of hearing
Active mechanics of hair cells
Cochlear waves
Signal amplification by nonlinear oscillators
Research Highlights
Chemically Active Wetting
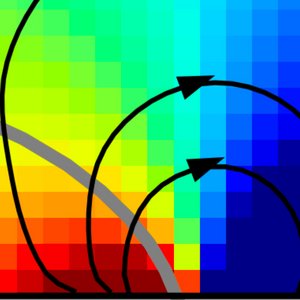
We consider chemically active wetting as a class of systems, where a condensed phase wets a surface and surface interactions are active. Activity is due to binding and detachment of molecules that are maintained away from equilibrium. We show that non-equilibrium conditions at the triple line give rise to long range chemical potential fields that govern the droplet shape. Resulting droplet shapes similar to pancake or mushroom can emerge and contact angles can vary with kinetic rates. Our work could be relevant to biological condensates that interact with surfaces such as membranes in the cell.
S. Liese, X. Zhao, C. A. Weber and F. Jülicher
Proc. Natl. Acad. Sci. USA 122, e2403083122 (2025)
[PDF (11,8 MB)]
Active Loop Extrusion Guides DNA-Protein Condensation
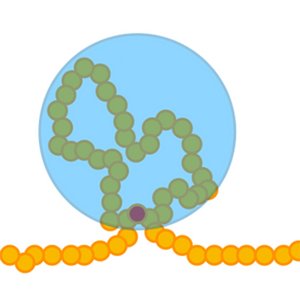
Long DNA molecules can be organized in space by active processes such as loop extrusion, where a DNA loop is pulled by a motor with the loop ends kept together. Spatial organization can also be achieved by co-condensation of proteins and DNA, forming a dense phase that packs the DNA. We study the interplay of loop extrusion and co-condensation and show that loop extrusion can facilitate nucleation of condensates, accelerate coarsening dynamics and position condensates to specific sites on DNA to which loop extruding motors bind. Our works reveals that DNA condensates can be efficiently organized using loop extrusion processes.
R. Takaki, Y. Savich, J. Brugués and F. Jülicher
Phys. Rev. Lett 134, 128401 (2025)
[PDF (2,6 MB)]
Nonequilibrium Transitions in a Template Copying Ensemble
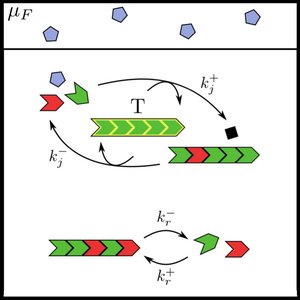
We study the process of template copying in a simple stochastic model and show that in the limit of long sequences, dynamic phase transitions between ensembles of random copies and accurate copies emerge as a function of fuel driving and copying specificity. We furthermore identify the minimal free energy supply required to maintain a population of accurate copies.
A. Genthon, C. D. Modes, F. Jülicher and S. W. Grill
Phys. Rev. Lett 134, 068402 (2025)
[PDF (457 kb)]
Concentration Buffering and Noise Reduction in Non-equilibrium Phase-separating Systems
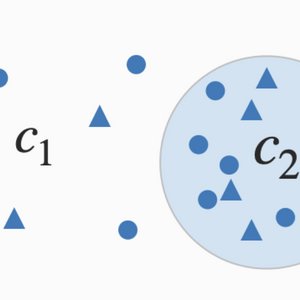
Phase separated condensates in cells can buffer concentrations and they can reduce concentration noise. We clarify the distinction between concentration buffering and noise reduction and show that in our of equilibrium conditions noise reduction can be effective even if concentrations are not buffered.
C. Zechner and F. Jülicher
Cell Systems 16, 101168 (2025)
[PDF (3 MB)]
Chemical Reactions Regulated by Phase-Separated Condensates

Biomolecular condensates provide distinct biochemical compartments in the cell. We investigate the regulation of chemical kinetics by phase-separated condensates. To this end, we introduce a framework for the case where the phase separation of scaffold molecules decouples from the reaction kinetics of client molecules. We discuss two examples of chemical processes, mono-molecular and bi-molecular reactions, and show that at an optimal condensate volume, reaction yield is maximized.
S. Laha, J. Bauermann, F. Jülicher, T. C. T. Michaels and C. A. Weber
Phys. Rev. Research 6, 043092 (2024)
[PDF (1,4 MB)]
Theory of Wetting Dynamics with Surface Binding
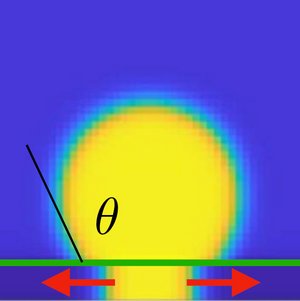
Biological condensates often interact with surfaces such as membranes. this can involve molecules that bind to the membrane and form a bound surface layer. we study the dynamics of phase separation near a surface, taking into account surface binding. We find different dynamic regimes and show that the bound layer can significantly accelerate wetting dynamics
X. Zhao, S. Liese, A. Honigmann, F. Jülicher and C. A. Weber
New J. Phys. 26, 103025 (2024)
[PDF (2,3 MB)]
Condensate Formation in Chiral Lattice Gas
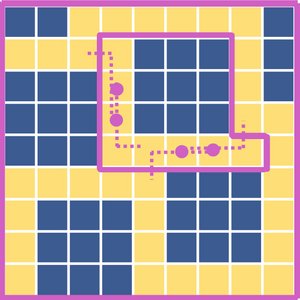
We study a lattice gas which can undergo phase separation and introduce chiral interactions. We explore a rich phase diagram that exhibits a cage and a fibre phase in addition to dense and dilute phases. Finally we discuss interfacial properties and surface tension for different interface types.
B. Wang, F. Jülicher and P. Pietzonka
New J. Phys. 26, 093031 (2024)
[PDF (3,7 MB)]
Active Shape Programming Drives Drosophila Wing Disc Eversion
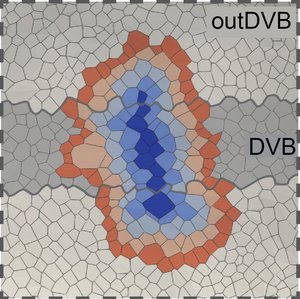
During fly wing morphogenesis the early fly wing undergoes a complex 3d remodelling where the tissue is everted. We use concepts from shape programmed materials to analyse the mechanics of eversion. Our work reveals that 3d tissue shape changes are largely driven by active anisotropic cell rearrangements which depend on myosin VI mediated mechanosensing.
J. F. Fuhrmann, A. Krishna, J. Paijmans, C. Duclut, G. Cwikla, S. Eaton, M. Popovic, F. Jülicher, C. D. Modes, N. A. Dye
Sci. Adv. 10, eapd0860 (2024)
[PDF (7,2 MB)]
Membrane Prewetting by Condensates Promotes Tight-Junction Belt Formation
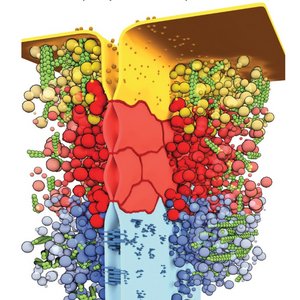
Epithelial tissues provide surfaces that are sealed and do not leak fluids. The confluence of such a tissue is enabled by tight cellular junctions between cells. We show that tight junctions form by a wetting phenomenon which promotes the assembly of a condensed protein layer around the apical membrane interface.
K. Pombo-García, O. Adame-Arana, C. Martin-Lemaitre, F. Jülicher and A. Honigmann
Nature 632, 647 (2024)
Charge Separation at Liquid Interfaces
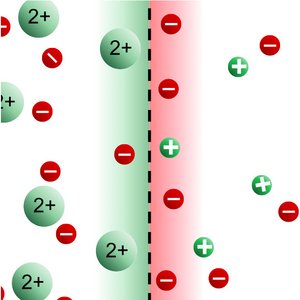
We discuss phase separation of fluids containing charged molecules. By combining a Flory Huggins model with electrostatics of charged components, we study charge density profiles. We find conditions where the charge density exhibits spatial periodicity at the interface.
A. Majee, C. A. Weber and F. Jülicher
Phys. Rev. Research 6, 033138 (2024)
[PDF (1,2 MB)]
Emergent Chirality in Active Solid Rotation of Pancreas Spheres

Pancreas derived cell spheres in a extracellular matrix environment exhibit spontaneous rotations. Interestingly, cell shape patterns of rotating spheres break chiral symmetry. Using theory and experiment, we show that spheres operate close to a yielding transition. Cell rearrangements and associated cell flows induce cell shape changes that reveal the underlying chirality of cell polarity patterns.
T. H. Tan, A. Amiri, I. Seijo-Barandiaran, M. F. Staddon, A. Materne, S. Tomas, C. Duclut, M. Popovic, A. Grapin-Botton and F. Jülicher
PRX LIFE 2, 033006 (2024)
[PDF (16,5 MB)]
Droplet Differentiation by a Chemical Switch

A fundamental question in biology is how biological condensates of different type can coexist in a cell. We present a minimal model of droplet differentiation, where phase separated droplets demix into two types with different chemical modifications triggered by enzymatic reactions.
X. Chen, R. Seyboldt, J.-U. Sommer, F. Jülicher and T. Harmon
Phys. Rev. Lett. 133, 028402 (2024)
[PDF (1,3 MB)]
A Cytokinetic Ring-Driven Cell Rotation Achieves Hertwig’s Rule in Early Development
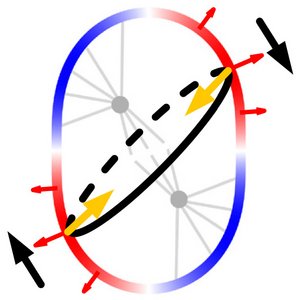
In 1884 Oscar Hertwigs suggested that cells divide along their long axis. We study the orientation of cell division in the embryo of the roundworm. We show that cortical stresses induce a torque which leads to rapid spindle rotation inside the cell.
T. C. Middelkoop, J. Neipel, C. E. Cornell, R. Naumann, L. G. Pimpale, F. Jülicher and S. W. Grill
Proc. Natl. Acad. Sci. USA 121, e2318838121 (2024)
[PDF (1,9 MB)]
Probe Particles in Odd Active Viscoelastic Fluids: How Activity and Dissipation Determine Linear Stability
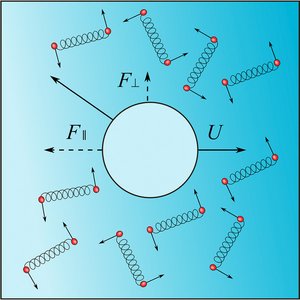
We consider a probe particle in a chiral visco-elastic material. Such a material can exhibit both odd viscosity and odd elasticity as well as passive and active behaviors. We discuss different regimes where the probe particle reveals the material properties in its response to external forces as well active regimes where, a resting probe particle is unstable even in the absence of a force.
C. Duclut, S. Bo, R. Lier, J. Armas, P. Surówka and F. Jülicher
Phys Rev. E. 109, 044126 (2024)
[PDF (1,8 MB)]
Core PCP Mutations Affect Short-time Mechanical Properties but not Tissue Morphogenesis in the Drosophila Pupal Wing
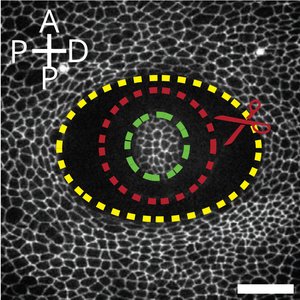
Epithelial tissues can exhibit polar asymmetries in the tissue plane that define morphological features such as the orientation of hairs. Tissues are often dynamic and can undergo anisotropic rearrangements and shear deformations. We show that the planar polarity system that defines the orientation of wing hairs in the fly influences cell mechanics but does not orient the overall axis of tissue shear.
R. Piscitello-Gómez, F. S. Gruber, A. Krishna, C. Duclut, C. D. Modes, M. Popovic, F. Jülicher, N. A. Dye, S. Eaton
eLife 12:e85581 (2023)
[PDF (7,6 MB)]
Odd Cosserat Elasticity in Active Materials
We discuss the behaviors of solid materials with unconventional active material properties. In addition to conventional Hookian elasticity, we consider a Cosserat elasticity, where torques are balanced by angular springs. This angular elasticity is combined with odd elasticity that can arise in active chiral materials. In combination these material properties enable wave-like modes with unusual properties.
P. Surówka, A. Souslov, F. Jülicher, and D. Banerjee
Phys. Rev. E 108, 064609 (2023)
[PDF (1,2 MB)]
Formation of Liquid Shells in Active Droplet Systems

We investigate for what conditions stable liquid shells form in the presence of chemical reactions in an active emulsion. We show that many stable shells can coexist. In a simple model of chemically active emulsions we find that droplets may either divide or rather from liquid shells, depending on parameters and conditions.
J. Bauermann, G. Bartolucci, J. Boekhoven, C. A. Weber, and F. Jülicher
Phys. Rev. Research 5, 043246 (2023)
[PDF (1 MB)]
Liquid Spherical Shells are a Non-equilibrium Steady State of Active Droplets
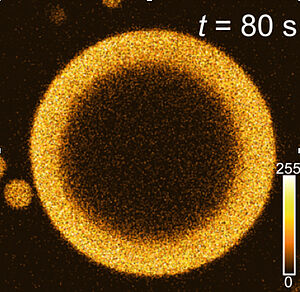
Phase separation leads to the formation of spherical droplets. Here we observe that in the presence of chemical reactions, liquid shells can emerge stable dissipative structures.
A. M. Bergmann, J. Bauermann, G. Bartolucci, C. Donau, M. Stasi, A-L. Holtmannspötter, F. Jülicher, C. A. Weber and J. Boekhoven
Nature Communications. 14, 6552 (2023)
[PDF (5 MB)]
Lift force in Odd Compressible Fluids
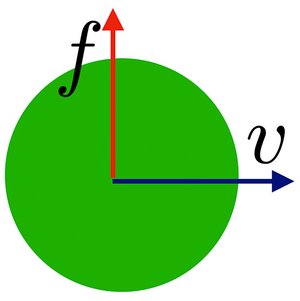
When a body moves through a fluid, it can experience a force orthogonal to its movement called lift force. We show that if the fluid is compressible, a lift force exists for a body moving in a material with odd viscosity.
R. Lier, C. Duclut, S. Bo, J. Armas, F. Jülicher and P. Surówka
Phys. Rev. E. 108, L023101 (2023)
[PDF (416 kB)]
Random Traction Yielding Transition in Epithelial Tissues

We investigate how randomly oriented cell traction forces lead to flow transition in a vertex model of epithelial tissues. We show that this transition is similar to a yielding transition of amorphous solids.
A. Amiri, C. Duclut, F. Jülicher and M. Popovic
Phys. Rev. Lett., 131, 188401 (2023)
[PDF (707 kB)]
Theory of Rheology and Aging of Protein Condensates
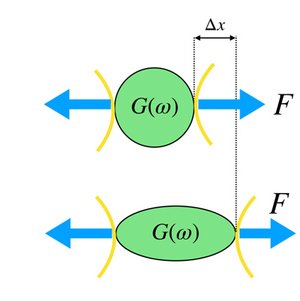
We show that a simple trap model can account for the glassy dynamics observed for ageing protein condensates.
R. Takaki, L. Jawerth, M. Popovic and F. Jülicher
PRX Life, 1, 013006 (2023)
[PDF (1,7 MB)]
Polarized Branched Actin Modulates Cortical Mechanics to Produce Unequal-size Daughters during Asymmetric Division
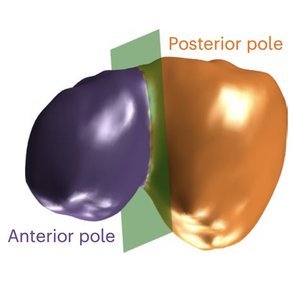
Here we study the role of cortical mechanics and material properties in the control of cell shape and size during asymmetric cell division. We show that by engineered mistargeting of the machinery for actin dynamics we can control the daughter cell size. Our work shows that the modulation of cortex bending rigidity plays a key role in regulating cell size asymmetry during division.
A. Daeden, A. Mietke, E. Derivery, C. Seum, F. Jülicher and M. Gonzalez-Gaitan
Nature Cell Biology 25, 235 (2023)
[PDF (18,5 MB)]
Heat Fluctuations in Chemically Active Systems

Living matter hosts a multitude of metabolic processes which are out of equilibrium and generate heat. Here we consider a simple model of reaction events with Poisson statistics in space and time, each releasing a small ampunt of heat. We study the resulting heat and temperature fluctuations and compare them to thermal fluctuations in passive systems. This comparison reveals length and time scales that are dominated by active fluctuations as well as passive dominated regimes where local equilibrium conditions hold. Our work provides a framework to discuss local equilibrium conditions and active dominated regimes in living matter.
J. Mabillard, C. A. Weber and F. Jülicher
Phys. Rev. E 107, 014118 (2023)
[PDF (574 kB)]
Topological Morphogenesis of Neuroepithelial Organoids

Organoids are simple multicellular model systems that recapitulate basic features of developmental processes in three dimensions. We study the morphogenesis of neuroepithelia and show that it can be regulated by retinoic acid signaling. Depending on signaling levels different epithelial topology emerges during morphogenesis. We show that the time course of topology is regulated by the relative importance of trans and cis-fusion events. We speculate that this sensitivity to topology could involve a control of gaussian bending rigidity of the epithelium.
K. Ishihara, A. Mukherjee, E. Gromberg, J. Brugués, E. M. Tanaka and F. Jülicher
Nature Physics 19, 177-183 (2023)
[PDF (5,1 MB)]
Broken Living Layers: Dislocations in Active Smectic Liquid Crystals
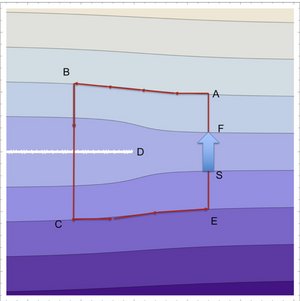
Smectics are systems with a one-dimensional crystalline or periodic order. Such layered systems can exhibit topological defects which often lead to loss of order as a result of fluctuations. Here we discuss the large-scale order in active smectics that are maintained away from thermal equilibrium. In such systems topological defects tend to move but as we show they do not move in a homeostatics state. We find that active smectics are less robust against noise than passive ones but order can persist for weak noise if rotation invariance is broken.
F. Jülicher, J. Prost and J. Toner
Phys. Rev. E 106, 054607 (2022)
[PDF (631 kB)]
Chemical Kinetics and Mass Action in Coexisting Phases
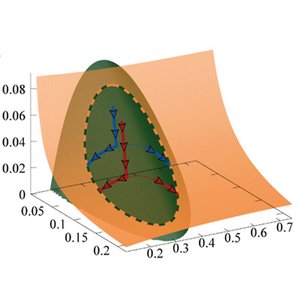
Chemical reactions are driven by differences in chemical potentials between substrates and products. Chemical potentials also govern phase separation phenomena and droplet formation. Here we discuss chemical processes organized by droplets. We show that mass action laws have to be modified in a thermodynamic consistent way when liquid phases coexist and discuss how non-equilibrium conditions can be induced by chemical fuels and chemostat boundary conditions. Our work provides a general framework to study biochemical processes in membraneless compartments.
J. Bauermann, S. Laha, P. M. McCall, F. Jülicher and C. A. Weber
J. Am. Chem. Soc, 144, 19294 (2022)
[PDF (3,2 MB)]
Long-range Morphogen Gradient Formation by Cell-to-Cell Signal Propagation
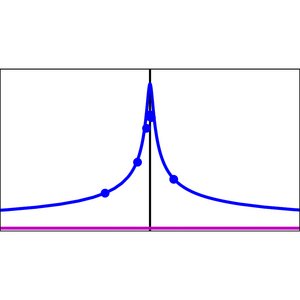
We study the formation of morphogen gradients by signal propagation where morphogen signaling induces cells to secrete morphogen. In such a system the delay length of gradients can exceed the distance individual morphogen molecules travel before they are degraded. Interestingly, when ligands are secreted asymmetrically, an effective drift emerges in the coarse-grained description of morphogen profiles even though molecules do not drift. We show that the feedback strength of signaling can be used by cells to regulate the gradient decay length over large ranges.
J. E. M. Dickmann, J. C. Rink and Frank Jülicher
Phys. Biol. 19, 066001 (2022)
[PDF (4 MB)]
Energy and Matter Supply for Active Droplets
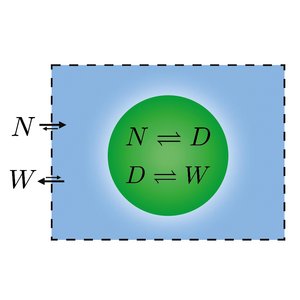
We present a general theory of active droplets that are driven out of equilibrium by chemical fuels or reservoirs. Using this approach, we discuss simple scenarios of active droplets that exhibit properties similar to cells such as growth and division. We discuss fluxes of energy and matter that obey conservation laws and show that such systems exhibit a rich interplay of exo and endothermal reaction behaviors together with latent heat at interfaces.
J. Bauermann, C. A. Weber and F. Jülicher
Ann. Phys. (Berlin)534, 2200132 (2022)
[PDF (1,4 MB)]
A Condensate Dynamic Instability Orchestrates Actomyosin Cortex Activation
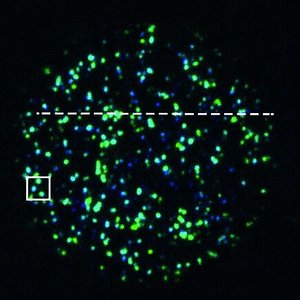
We show that the activation of the acto-myosin network of oocytes involves the formation of large numbers of dynamic condensates that first grow and subsequently shrink and disassemble. This phenomenon represents an example of active condensates that are chemically driven. Condensate dynamics follow mass action kinetics that governs both composition and size. This dynamic instability and transient condensate formation could allow the cell to keep control over autocatalytic filament assembly during the activation of the actin network.
V. T. Yan, A. Narayanan, T. Wiegand, F. Jülicher and S. W. Grill
Nature 609, 597 (2022)
[PDF (17 MB)]
Flagella-like Beating of Actin Bundles Driven by Self-organized Myosin Waves
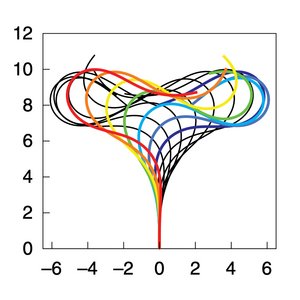
Many cells possess motile cilia or flagella that generate oscillations and propagating mechanical waves to induce fluid flows or to swim. Here we show that filaments in the presence of molecular motors can spontaneously self-organize to generate oscillations and waves including density waves of motors. We present a simple theory that can account for the experimental observations.
M. Pochitaloff, M. Miranda, M. Richard, A. Chaiyasitdhi, Y. Takagi, W. Cao,E. M. De La Cruz, J. R. Sellers, J.-F. Joanny, F. Jülicher, L. Blanchoin and P. Martin
Nature Physics, 18, 1240 (2022)
[PDF (8,6 MB)]
Active T1 Transitions in Cellular Networks
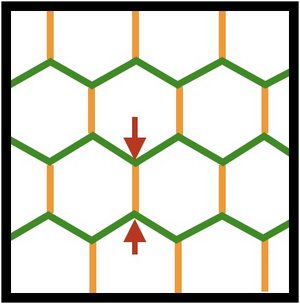
Developing tissues are active materials that can change their shape by spontaneous shear deformations. Such tissue shear involves cell rearrangements via T1 transitions by which cells change their neighbors. These cell rearrangements can be driven by active stresses such as contractile tension of cell bonds. Here we show that the axis of induced shear can depend on where active stress acts in the cell. We furthermore discuss the energetics of active shear and distinguish active from passive T1 transitions, depending on whether they perform work on the tissue or whether they dissipate energy.
C. Duclut, J. Paijmans, M. M. Inamdar, C. D. Modes and F. Jülicher
Eur. Phys. J. E 45, 29 (2022)
[PDF (1,2 MB)]
Molecular Assembly Lines in Active Droplets
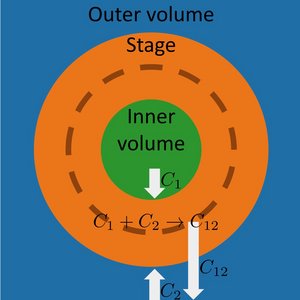
A fundamental question in biology is how complexes of several molecules can reliably assemble. Here we show that a molecular assembly line can be self-organized by active droplets where it can form spontaneously. This assembly line arranges different assembly steps spatially so that a specific order of assembly is achieved and incorrect assembly is suppressed. We show how assembly bands are positioned and controlled and discuss the rate and fidelity of assembly as compared to other assembly scenarios.
T. S. Harmon and F. Jülicher
Phys. Rev. Lett. 128, 108102 (2022)
[PDF (602 kB)]
Coarse-grained Curvature Tensor on Polygonal Surfaces
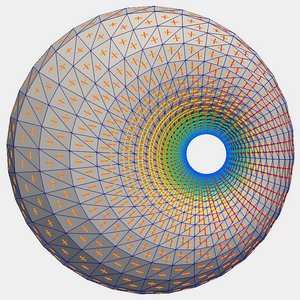
Complex morphologies and geometries in biology are formed from many individual subunits such as cells. Therefore, in theoretical approaches to morphogenesis, shapes are sometimes represented by polygonal elements. However, ideally shapes are captured continuously by differential geometry. Here using concepts from integral geometry, we show that on a discrete surface coarse grained curvature tensors can be robustly defined that converge to the corresponding continuum object when the discretization is refined.
C. Duclut, A. Amiri, J. Paijmans and F. Jülicher
SciPost Phys. Core 5, 011 (2022)
[PDF (8,2 MB)]
Co-condensation of Proteins with Single- and Double-stranded DNA

We show that FUS proteins, which are known to form liquid-like condensates in buffer solution, can bind to DNA and form DNA-protein condensates. Such condensates form with single stranded DNA that peels off stretched DNA in a force dependent manner. Double stranded DNA also condenses together with FUS proteins at small tension and exerts capillary forces that can be measured directly. Protein-DNA co-condensation provides a mechanosensitive organization of DNA and proteins that could be relevant for cellular processes such as DNA repair.
R. Renger, J. A. Morin, R. Lemaitre, M. Ruer-Gruss, F. Jülicher, A. Hermann and S. Grill
Proc. Natl. Acad. Sci. USA 119, e2107871119 (2022)
[PDF (2,6 MB)]
Hydrodynamics of Chiral Squirmers
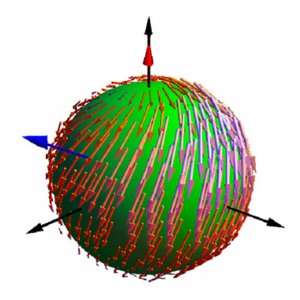
We consider a simple squirmer model of microswimmers with chiral asymmetries, which captures key features of swimming microorganisms. We show that these swimmers move on helical trajectories. When two swimmers interact via hydrodynamic interaction they can form bound states where they move together and their trajectories wind around each other. Our work reveals emergent behaviors of chiral active processes.
P.S. Burada, R. Maity and F. Jülicher
Phys Rev E 105, 024603 (2022)
[PDF (2,1 MB)]
A Gelation Transition Enables the Self-organization of Bipolar Metaphase Spindles
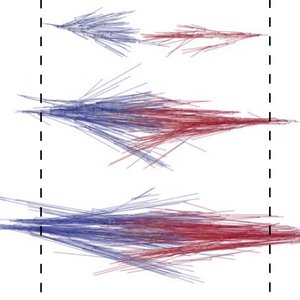
We study the interplay of dynamic microtubules in the organization of the mitotic spindle. We find that the spindle can have solid-like properties and that two oppositely oriented gels can move relative to each other. Our work reveals very unconventional active material behaviors that govern spindle assembly.
B. A. Dalton, D. Oriola, F. Decker, F. Jülicher and J. Brugués
Nature Physics 18, 132 (2022)
[PDF (5,5 MB)]
Sequence-dependent Surface Condensation of a Pioneer Transcription Factor on DNA

We show that key proteins involved in gene regulation can form small condensates on DNA. This condensation can be understood in the framework of wetting phenomena on heterogeneous substrates. We find that condensation depends on DNA sequence and key features of the condensation pattern can be captured by a heterogeneous Ising model. We show that condensation on DNA can provide a collective and robust readout of DNA sequence information.
J. A. Morin, S. Wittmann, S. Choubey, A. Klosin, S. Golfier, A. A. Hyman, F. Jülicher and S. W. Grill
Nature Physics 18, 271 (2022)
[PDF (10,9 MB)]
Morphogen Gradient Scaling by Recycling of Intracellular Dpp
Using a combination of several quantitative assays, we show that the transport of morphogens in the developing fly wing relies on extracellular diffusion, internalization and recycling of molecules. We show that in this transport regime the gradient decay length can be regulated by modulating the kinetics of molecular binding to receptors. This provides a general mechanism to achieve scaling of morphogen gradients during tissue growth.
M. Romanova Michailidi, Z. Hadjivasiliou, D. Aguilar-Hidalgo, D. Basagiannis, C. Seum, M. Dubois, F. Jülicher and M. Gonzalez-Gaitan
Nature 602, 287 (2022)
[PDF (37,2 MB)]
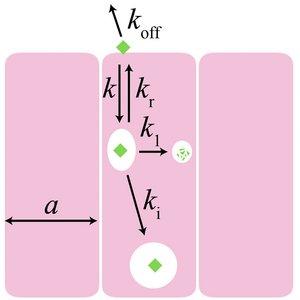
Stochastic Dynamics of Single Molecules across Phase Boundaries
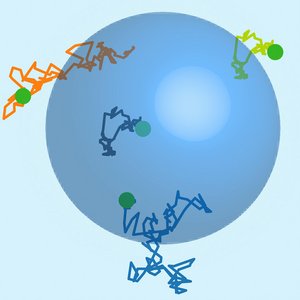
Phase boundaries separate coexisting liquid phases of different composition. Here we study the stochastic motion of molecules that diffuse in a phase separated liquid. We show that trajectories can be described by a Langevin equation with a drift term that captures effects of molecular interactions. We show that the statistics of displacements across a phase boundary can reveal phase separation parameters. Interestingly, single molecules in concentration gradients can on average move in a direction opposite to the flux of collective diffusion.
S. Bo, L. Hubatsch, J. Bauermann, C. A. Weber and F. Jülicher
Phys. Rev. Research 3, 043150 (2021)
[PDF (1,1 MB)]
Nonlinear Rheology of Cellular Networks
Tissues are active soft materials with complex material properties. They can exhibit an elastic response to stress. Furthermore, cell rearrangements and cell neighbor exchanges can give rise to tissue flow and viscous material properties. We discuss the response of a tissue to external shear using a vertex model that takes into account cell shape fluctuations. We show that the rheology of such a tissue can be captured accurately by a nonlinear continuum description based on simple and general principles.
C. Duclut, J. Paijmans, M. M. Inamdar, C. D. Modes, and F. Jülicher
Cells and Development 168, 203746 (2021)
[PDF (3,5 MB)]
Thermodynamics of Wetting, Prewetting and Surface Phase Transitions with Surface Binding
Wetting phenomena occur when liquids interact with surfaces, promoting surface layers or giving rise to contact angles for droplets. In cells, liquid-like condensates can interact with surfaces such as membranes and exhibit wetting. Condensates form when certain proteins assemble in a liquid phase. Often such proteins are also able to bind to a membrane. Here we study how wetting behaviors are influenced by surface binding of molecules. We show that the existence of a bound layer below the wetting layer can give rise to a variety of novel phases and phase transitions on the surface. This could have implications for the organization of biochemical processes near membranes.
X. Zhao, G. Bartolucci, A. Honigmann, F. Jülicher and C. Weber
New J. Phys. 23,123003 (2021)
[PDF (3,7 MB)]
Local Thermodynamics Govern Formation and Dissolution of Caenorhabditis elegans P Granule Condensates
In living cells, biochemical processes can be localized in liquid-like droplets which are condensates of proteins and nucleic acids such as RNA. We show that condensates called P granules assemble and disassemble in response to temperature changes in a way that is consistent with a thermodynamic phase separation process. We estimate the effects of active process to perturb local thermodynamic conditions. We provide arguments that in small local volume elements a thermodynamic is quickly reached, while at larger scales the cell interior is maintained out of equilibrium. Overall, our work shows that the cell harbors active emulsions of phase separated droplets that spatially organize biochemistry.
A. W. Fritsch, A. F. Diaz-Delgadillo, O. Adame-Arana, C. Hoege, M. Mittasch, M. Kreysing, M. Leaver, A. A. Hyman, F. Jülicher, and C. A. Weber
PNAS 118 (37) (2021)
[PDF (1,8 MB)]
Quantifying Entropy Production in Active Fluctuations of the Hair-Cell Bundle from Time Irreversibility and Uncertainty Relations

Hair bundles are the mechanical sensors of sensory cells of the ear. They use active processes to amplify weak signals to detect sound in the ear of vertebrates. We study the activity of spontaneously oscillating hair bundles and quantify the time reversal asymmetry as a measure of irreversibility and dissipation. We find on average a lower bound on entropy production of about 3k_B/s, revealing the active nature of the spontaneous movements.
É. Roldán, J. Barral, P. Martin, J. M R Parrondo, and F. Jülicher
New J. Phys. 23, 083013 (2021)
[PDF (4,1 MB)]
Force Generation by Protein–DNA Co-Condensation
Many proteins bind to DNA. This is important for key cellular processes such as gene expression. Here we show that co-condensation of proteins and DNA can lead to the formation of small spherical condensates that exert forces on the free DNA that remains outside. A simple droplet model that takes into account surface tension and bulk free energy can quantitatively account for the observed forces and their dependence on DNA length. Our results suggest that condensation forces could play a role in chromatin organization.
T. Quail, S. Golfier, M. Elsner, K. Ishihara, V. Murugesan, R. Renger, F. Jülicher, and J. Brugués
Nature Physics 17, 1007 (2021)
[PDF (11,6 MB)]
A Hydraulic Instability Drives the Cell Death Decision in the Nematode Germline
Newly formed oocytes in the gonad of the roundworm are large cells which grow at the expense of other precursor cells that shrink and disappear. Which cells are selected to become mature oocytes and which ones disappear by cell death, is a fundamental question in biology. Here we show that the transition between growth and shrinkage results from a hydraulic instability that breaks symmetry between cells spontaneously, driven by pressure differences and fluid flows. This suggests that it is not primarily chemical signals that trigger this life and death decision but rather a physical instability.
N. T. Chartier, A. Mukherjee, J. Pfanzelter, S. Fürthauer, B. T. Larson, A. W. Fritsch, R. Amini, M. Kreysing, F. Jülicher, and S. W. Grill
Nature Physics 17, 920 (2021)
[PDF (7,3 MB)]
Hydraulic and Electric Control of Cell Spheroids
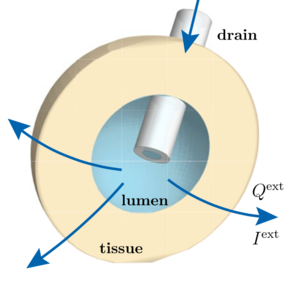
Multicellular spheroids are models for the dynamics and the material properties of tissues or tumors. Here we show using a generic theory of spheroid dynamics that externally imposed electric currents or fluid flows could be used to control growth dynamics and size of cell spheroids. Such currents or flows could be applied using for example micropipettes or small tubes. Our work has potential applications in medicine and could be used to suppress tumors.
C. Duclut, J. Prost, and F. Jülicher
Proc. Natl. Acad. Sci. U.S.A. 118, e2021972118 (2021)
[PDF (0,2MB)]
Self-Organized Patterning of Cell Morphology via Mechanosensitive Feedback

Cells often exhibit elongated shapes and such cell elongation can form patterns in a tissue. Here we investigate the origins of such patterns in cell shape. We show that in the developing fly wing patters of anisotropic active processes induce oriented cell rearrangements which in turn drive cell elongation in patterns with a radial symmetry. Our work reveals a general mechanism for the emergence of cell shape patterns in tissues.
N. A. Dye, M. Popovic, K. V. Iyer, J. Fuhrmann, R. Piscitello-Gómez, S. Eaton, and F. Jülicher
eLife 10:57964 (2021)
[PDF (30,8 MB)]
Apico-Basal Cell Compression Regulates Lamin A/C Levels in Epithelial Tissues
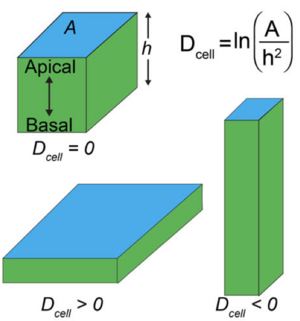
Tissues can transduce mechanical stimuli to chemical signals that are processed in the cell. Lamins form filaments in the nucleus that provide a scaffold. These filaments are involved in machano transduction. Here we show that the amount of lamins in the nucleau are controlled by cell shape and change if cells are compressed along the apical basal axis.
K. V. Iyer, A. Taubenberger, S. A. Zeidan, N. A. Dye, S. Eaton, and F. Jülicher
Nature Communications 12, 1756 (2021)
[PDF (6,6 MB)]
Active Viscoelasticity of Odd Materials
We discuss the active matter with chiral asymmetries. Active chiral systems can have unconventional material properties. Generalizing the concepts of odd viscosity and odd elasticity to rheology, we characterize visco-elastic systems with chiral frequency dependent odd moduli. We show that such systems exhibit wave-like modes with speeds and damping set by the odd elastic coefficient.
D. Banerjee, V. Vitelli, F. Jülicher, and P. Surówka
Phys. Rev. Lett. 126, 138001 (2021)
[PDF (0,5 MB)]
Theory of Time Delayed Genetic Oscillations with External Noisy Regulation
We present a general model for the noisy dynamics of genetic oscillations such as the circadian clock or the segmentation oscillator.
Our work shows that genetic oscillations with diverse biological contexts can be understood in a common framework based on a delayed negative feedback system
and regulator dynamics.
J. Negrete Jr, I. M. Lengyel, L. Rohde, R. A. Desai, A. C. Oates, and F. Jülicher
New J. Phys. 23, 033030 (2021); https://doi.org/10.5281/zenodo.7584248
[PDF (2,8 MB)]
Transcription Organizes Euchromatin via Microphase Separation
DNA is packed in the cell nucleus together with many proteins in the form of chromatin. This chromatin is very dynamic and the chromatin is spatially organized in inactive domains and pockets of activity where genetic information is read and transcribed to RNA. Here we show that the organization of active domains can be described as a microphase separation phenomenon in an active system. This microphase separation can account for the formation of many small domains which do not coarseninto larger structures.
L. Hilbert, Y. Sato, K. Kuznetsova, T. Bianucci, H. Kimura, F. Jülicher, A. Honigmann, V. Zaburdaev, and N. L. Vastenhouw
Nature Communications 12, 1360, (2021)
[PDF (5,6 MB)]
Epithelial Colonies In Vitro Elongate through Collective Effects
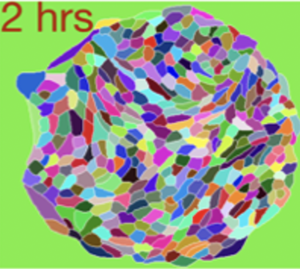
We study the spontaneous elongation of spreading cell sheets in vitro and show that this elongation results from anisotropies in average cell shapes. THese anisotropies are self-organized in a nematic field over larger scales and determine in which direction the cell sheet expands. Our work reveals principles of collective dynamics of cellular assemblies.
J. Comelles, SS Soumya, L. Lu, E. Le-Maout, S. Anvitha, G. Salbreux, F. Jülicher, M. M Inamdar, D. Riveline
eLife 10:e57730 (2021)
[PDF (27,7 MB)]
Continuum Theory of Active Phase Separation in Cellular Aggregates
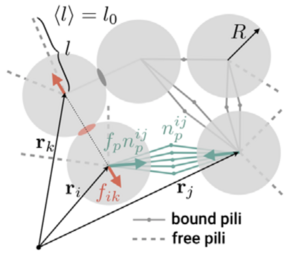
We propose a continuum theory for cell assemblies that interact via pulling forces of pili. We show that this aggregate formation can be described as a phase separation process in an active system. This system can exhibit damped oscillations and rich rheological properties. Our theory can ccount for the collectiev dynamics of N. gonorrhoeae bacteria.
H.-S. Kuan, W. Pönisch, F. Jülicher, and V. Zaburdaev
Phys. Rev. Lett. 126, 018102 (2021)
[PDF (1,7 MB)]
Quantification of Nematic Cell Polarity in Three-dimensional Tissues
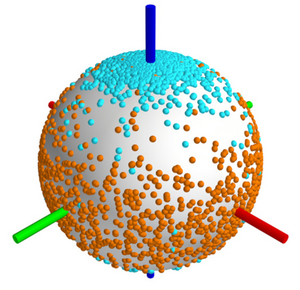
Tissues are soft materials formed by large numbers of cells which often are amorphous. However there is order underlying the seeming randomness of many cell packings. Here we present a general approach that reveals biaxial nematic cell polarity as an order parameter characterizing liver tissue structure. This biaxial order is coordinated
at large scales and relates to the function of the liver based two separate but interpenetrating transport networks.
A. Scholich, S. Syga, H. Morales-Navarrete, F. Segovia- Miranda, H. Nonaka, K. Meyer, W. de Back, L. Brusch, Y. Kalaidzidis, M. Zerial, F. Jülicher, B. M. Friedrich
PLOS Computational Biology 17, e1009349 (2020)
[PDF (6,8 MB)]
Protein Condensates as Aging Maxwell Fluids
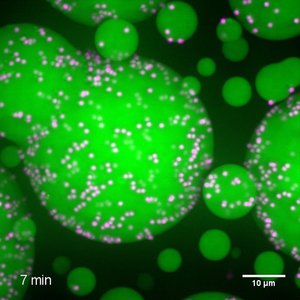
Cells organize their biochemistry by forming liquid-like condensates of biomolecules that can act as tiny reactors to localize chemical reactions. Researchers from the Physics of Complex Systems together with with colleagues of the MPI of molecular cell biology and genetics in Dresden investigate the physical nature and material properties of protein condensates using microrheology techniques. They find that many protein condensates increase their viscosity with time and slow their dynamics, while always remaining soft and liquid-like. This is suggestive of glassy behaviors and could have important implications for cellular dynamics.
L. Jawerth, E. Fischer-Friedrich, S. Saha, J. Wang, T. Franzmann, X. Zhang, J. Sachweh, M. Ruer, M. Ijavi, S. Saha, J. Mahamid, A. A. Hyman, F. Jülicher
Science 370, 1317 (2020)
[PDF (2 MB)]
Extreme-Value Statistics of Stochastic Transport Processes
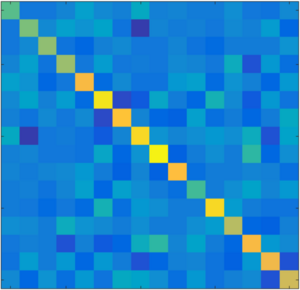
When a molecular motor moves stochastically along a track it has an average speed but somtimes speeds up, slows down or may even occasionally move backwards. Here we study the statistics of extrema of distance traveled during a given time. We discover a relationship between relaxation time spectra of extreme value statistics and eigenvalue spectra of random matricies. We show that random matricies can be used to efficiently generate extrema distributions. Our work provides new insights in the stochastic thermodynamics of transport processes.
A. Guillet, E. Roldan, and F. Jülicher
New J. Phys. 22, 123038 (2020)
[PDF (1,8 MB)]
Power-Law Population Heterogeneity Governs Epidemic Waves
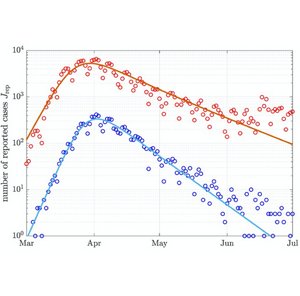
We generalize the classical Susceptible-Infected-Removed (SIR) model of epidemic waves to take into account population heterogeneity. We introduce a single new paramete that captures a distribution of the susceptibility of individuals to become infected. This generalized model has the same mathematical and computational complexity as the original model and can be solved exactly. We show that for a broad distribution of infection susceptibility herd immunity is reached faster than usually expected.
J. Neipel, J. Bauermann, S. Bo, T. Harmon, and F. Jülicher
PLoS ONE 15(10), e0239678, doi: 10.1371/journal.pone.0239678 (2020)
[PDF (2,8 MB)]
Liquid Phase Separation Controlled by pH
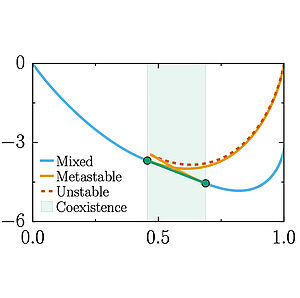
We study effects of solution pH on the phase separation of macromolecules. Chemical changes associated with proton exchange with water modify the charge state of the macromolecules and thereby the strength of molecular interactions. We predict a reentrant behavior as a function of pH and show that the region of phase separation is typically broader near the isoelectric point. Our work could accouont for the behaviors of proteins that form liquid like condensates in cells.
O. Adame-Arana, C. A. Weber, V. Zaburdaev, J. Prost, and F. Jülicher
Biophys. J. 119, 1590 (2020)
[PDF (1,9 MB)]
Flagellar Length Control in Biflagellate Eukaryotes: Time-of-flight, Shared Pool, Train Traffic and Cooperative Phenomena
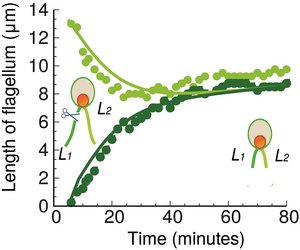
Flagella are hair-like appendages of many eucaryotic cells. They grow via the assembly of new building blocks that are transported to the tip by a intraflagellar transport via molecular motors. A key question is to understand how flagellar length is regulated. We present a stochastic model of flagellar lwngth control where flagellar length is regulated via the time of travel from the base to the tip and back. We relate our theory to experiments and make predictions for flagellar length fluctuations.
S. Patra, F. Jülicher, and D. Chowdhury
New J. Phys. 22, 083009 (2020)
[PDF (6,5 MB)]
Active Forces Shape the Metaphase Spindle through a Mechanical Instability
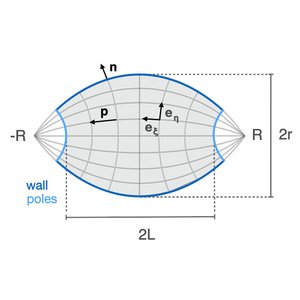
The mitotic spindle has a fundamental role in cell division and physically separated the duplicated chromosomes to distribute them reliably in two daugther cells. The spindle can be understood as an active liquid crystal in which microtubules are aligned in a bipolar organization and molecular motors generate active stresses. Here we show that the shape of the spindle results through a mechanical instability by an interplay of active stresses in the bulk and at the surface. Our work reveals how motor proteins can mold liquid crystalline droplets, and has implications for the design of active soft materials.
D. Oriola, F. Jülicher, and J. Brugués
Proc. Natl. Acad. Sci. USA 117,16154 (2020)
[PDF (1,2 MB)]
BMP Signaling Gradient Scaling in the Zebrafish Pectoral Fin
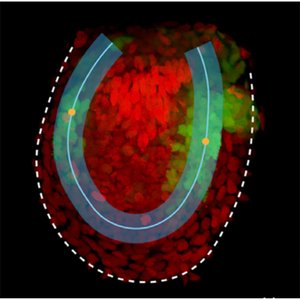
Morphogen gradients are involved in the patterning of developing tissues and also in the regulation of tissue growth. Here we study the development and growth of the zebrafish fin. We show that the profile shape and the amplitude of BMP signaling activity scales with tissue length. This scaling behavior is consistent with a growth control scenario by which relative rates of change of a signal promote tissue growth.
R. Mateus, L. Holtzer, C. Seum, Z. Hadjivasiliou, M. Dubois, F. Jülicher, and M. Gonzalez-Gaitan
Cell Report 30, 4292 (2020)
[PDF (4,9 MB)]
Phase Separation Provides a Mechanism to Reduce Noise in Cells
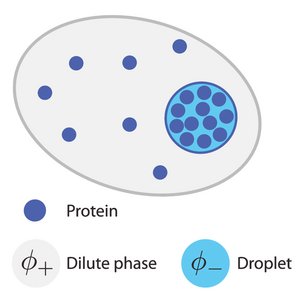
Phase coexistence between a droplet and a surrounding fluid can keep concentration levels within a narrow range. Here we show the physics of phase separation provides a general mechanism to buffer and reduce thermal and active concentration fluctuations in cells.
A. Klosin, F. Oltsch, T. Harmon, A. Honigmann, F. Jülicher, A. A. Hyman and C. Zechner
Science 367, 464 (2020)
[PDF (1,9 MB)]
Casimir Stresses in Active Nematic Films
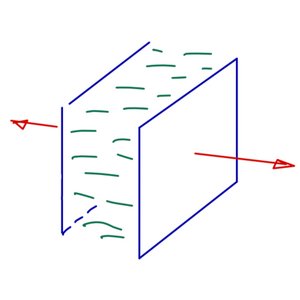
Casimir forces are fluctuation-induced forces that act between two parallel surfaces. The classical example are weak attractive interactions between conducting surfaces due to fluctuations of the electromagnetic field. Casimir stresse between surfaces due to thermal fluctuations can be studied in condensed matter systems such as liquid crystals. Here we investigate the Casimir stresses resulting from fluctuations in active nematics.
A. Basu, J.-F. Joanny, F. Jülicher and J. Prost
New J. Phys. 21, 123046 (2019)
[PDF (541 kB)]
Minimal Model of Cellular Symmetry Breaking
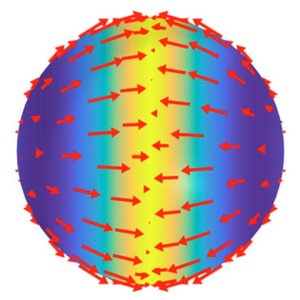
We discuss the mechano-chemical self-organization of an active fluid on a spherical sur-face. We find that a minimal model can generate patterns of flow, concentration and stress that exhibit key features of fundamental cellular processes such as cell symmetry breaking, cell division and cell locomotion. Furthermore, we show that this system provides insights in the mechanochemical self-organization of shapes. Our work thus provides a framework for the study of general principles of cellular self-organization.
A. Mietke, V. Jemseena, K. Vijay Kumar, I. F. Sbalzarini and F. Jülicher
Phys. Rev. Lett. 123, 188101 (2019)
[PDF (623 kB)]
Soluble Tubulin is Significantly Enriched at Mitotic Centrosomes
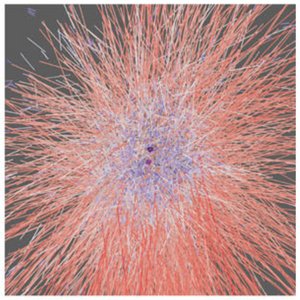
Centrosomes play an key role for the organization of the mitotic spindle and serve as sites of microtubule nucleation. In order to understand centrosomal nucleation of microtubules it is important to know whether centrosomes locally enrich soluble tubulin. Here we deter-mine the spatial distribution of filamentous and soluble tubulin near the centrosome and show that soluble tubulin is locally enriched in centrosomes. We quantify tubulin concentra-tion inside and outside the centrosome. Our work suggests that centrosomal microtubule nucleation is mediated by locally increased tubulin concentrations.
J. Baumgart, M. Kirchner, S. Redemann, A. Bond, J. Woodruff, J.-M. Verbavatz, F. Jülicher,
T. Müller-Reichert, A. A. Hyman and J. Brugués
J Cell Biol. 218, 3977 (2019)
[PDF (1,9 MB)]
Integral Fluctuation Relations for Entropy Production at Stopping Times
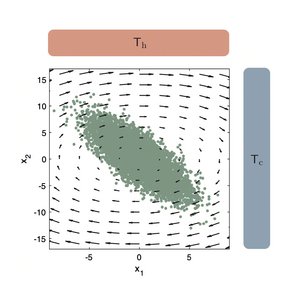
We discuss fluctuation theorems for non-equilibrium stochastic processes that follow from the Martingale property of the exponential of the stochastic entropy at stopping times. Our work reveals generic features of non-equilibrium processes.
I. Neri, E. Roldan, S. Pigolotti and F. Jülicher
J. Stat. Mech., 104006 (2019)
[PDF (2,9 MB)]
Fluid Pumping and Active Flexoelectricity can Promote Lumen Nucleation in Cell Assemblies
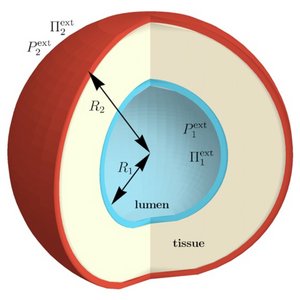
Fluid filled lumen often form in tissues during development. They can serve as transport channels such as in the liver or the pancreas. Here we discuss the physical principles under-lying the nucleation of lumen in spherical cell assemblies. We show that in some regimes lumen nucleation is similar to classical nucleation theory. Surprisingly, we also find that tissue ferroelectricity, the coupling of bending to electric fields, can facilitate lumen nuclea-tion. Our results show that electro-hydraulic effects could play an important role in tissue morphogenesis.
C. Duclut, N. Sarkar, J. Prost and F. Jülicher
Active Cargo Positioning in Antiparallel Transport Networks
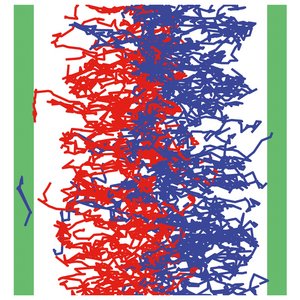
Using micropatterns of actin polymerization in vitro, we investigate stochastic transport of colloidal beads in antiparallel networks of overlapping actin filaments. A theoretical description of the system reveals the key physical rules for cargo transport and positioning in filament networks of mixed polarity.
M. Richard, C. Blanch-Mercader, H. Ennomani, W. Cao, E. M. De La Cruz J.-F. Joanny, F. Jülicher, L. Blanchoinc, and P. Martin
Liquid-Crystal Organization of Liver Tissue
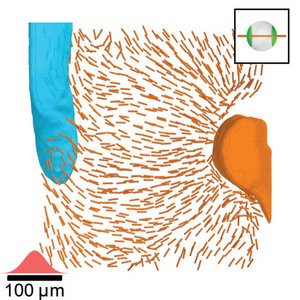
Three-dimensional tissues are amorphous arrangements of cells which can exhibit structural order that is linked to their function. Here, we investigate principles that underlie the organization of liver tissue. The liver has important metabolic functions that require transport networks of blood and bile that connect to liver cells. Here we show by quantifying cell polarity and cell nematics together with the morphology of transport networks that liver tissue has the organization of a nematic liquid crystal with large scale orientational order.
H. Morales-Navarrete, H. Nonaka, A. Scholich, F. Segovia-Miranda, W. de Back, K. Meyer, R. L. Bogorad, V. Koteliansky, L. Brusch, Y. Kalaidzidis, F. Jülicher, B. M. Friedrich, M. Zerial
eLife 8:e44860 (2019)
[PDF (5,1 MB)]
Field Induced Cell Proliferation and Death in a Model Epithelium
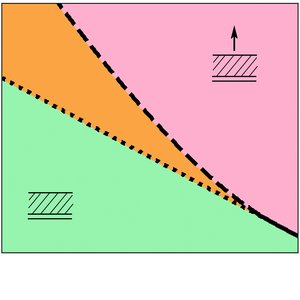
Epithelia are sheet like tissue layers. Here we present a theoretical study of the dynamics of a thick polar epithelium that is subjected to the action of both an electric field and a hydrodynamic flow that permeates the tissue. We develop a generalized continuum hydrodynamic description and describe the tissue as a two-component fluid system. Considering a planar geometry, we find that finite thickness tissue layers exist only in a restricted region of phase space and that relatively modest electric fields or imposed external flows can induce either proliferation or death.
N. Sarkar, J. Prost and F. Jülicher
New J. Phys. 21, 043035 (2019)
[PDF (1,2 MB)]
Extreme Reductions of Entropy in an Electronic Double Dot
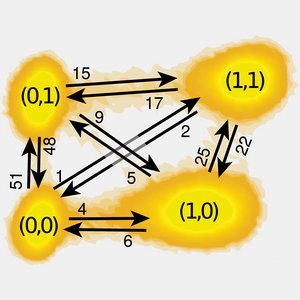
We study negative fluctuations of stochastic entropy production in an experimental system of a electronic double dot. The system operates at non-equilibrium steady-state conditions. We show that the average values of the minima of stochastic entropy production lie above the lower bound predicted by theory. We also extend our theory by deriving a general bound for the average value of the maximum heat absorbed by a mesoscopic system from the environment and compare this result with experimental data.
S. Singh, É. Roldán, I. Neri, I. M Khaymovich, D. S. Golubev, V. F. Maisi, J. T. Peltonen, F. Jülicher and J. P. Pekola
Phys. Rev. B 99, 115422 (2019)
[PDF (3,7 MB)]
Body size-dependent energy storage causes Kleiber’s law scaling of the metabolic rate in planarians
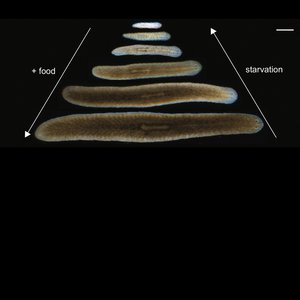
The metabolic rate of organisms varies with body mass. This dependence is well captured by a 3/4-power law scaling relation called Kleiber’s law. The physiological basis of Kleiber’s law are not understood. Here we show that the metabolic rate of flatworms obeys Kleiber’s law. In these animals Kleiber’s law does results from an increase of mass per cell with body mass but not from a decrease of metabolic rate per cell. An analysis of the energy balance combined with experiments shows that body size dependent energy stores are key to the emergence of Kleiber’s law in flatworms.
A. A. Thommen, S. Werner, O. Frank, J. Philipp, O. Knittelfelder, Y. Quek, K. Fahmy, A. Shevchenko, B. M. Friedrich, Frank Jülicher, J. C. Rink
eLife 2019;8:e38187 (2019)
[PDF (3,7 MB)]
Self-organized Shape Dynamics of Active Surfaces

Biological form emerges from dynamic processes that couple chemical signals to active mechanical processes. Here we present a simple framework to study the mechanochemical self-organization of surfaces. Surface shape is governed by force and torque balances in the presence of active surface stresses. These stresses are themselves regulated by diffusing molecular species. Our work reveals general principles of the mechano-chemical self-organization of geometries.
A. Mietke, F. Jülicher and I. Sbalzarini
Proc. Natl. Acad. Sci. USA, 116, 29 (2019)
[PDF (3,7 MB)]
Guiding Self-organized Pattern Formation in Cell Polarity Establishment
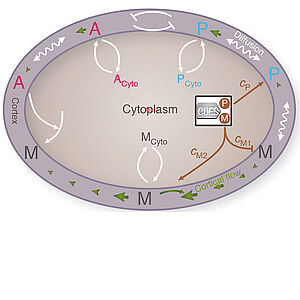
We present a quantitative theory of cell polarity establishment. Our model accounts for the dynamics of flows and concentration profiles in the cell cortex that emerge from mechano-chemical self-organization. We show that this self-organized process is guided by symmetry breaking cues. This system provides a paradynamic example for an important class of pattern forming systems in biology.
P. Gross, K. V. Kumar, N. W. Goehring, J. S. Bois, C. Hoege, F. Jülicher and S. W. Grill
Nature Physics, 15, 293 (2019)
[PDF (5,4 MB)]
Salt-Dependent Rheology and Surface Tension of Protein Condensates Using Optical Traps
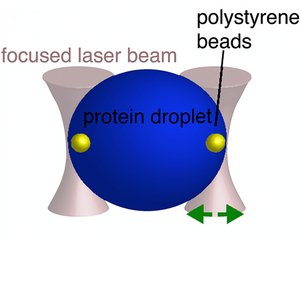
We develop a method based on optical tweezers to study the frequency dependent rheology of micron sized droplets. We use this method to determine the rheology of protein condensates that serve as simple models for membraneless organelles in cells. Our work shows that protein condensates are visco-elastic fluids with a viscosity that strongly depends on salt concentration.
L. M. Jawerth, M. Ijavi, M. Ruer, S. Saha, M. Jahnel, A. A. Hyman, F. Jülicher and E. Fischer-Friedrich
Phys. Rev. Lett 121, 258101 (2018)
[PDF (537 kB)]
Exactly Solvable Dynamics of Forced Polymer Loops
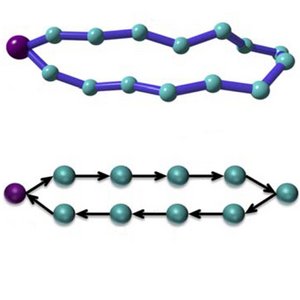
We consider a simple model of a closed polymer loop that is pinned at one point and is subject to an external force. We show that this model can be formally mapped to an asymmetric simple exclusion process. This link provides a link between the statistics of many particle systems and polymer physics. Our result can be applied to the dynamics of DNA loops under forcing.
W. Huang, Y. T. Ling, D. Frömberg, J. Shin, F. Jülicher and V. Zaburdaev
New J. Phys. 20, 113005 (2018)
[PDF (1,1 MB)]
Positioning of Particles in Active Droplets
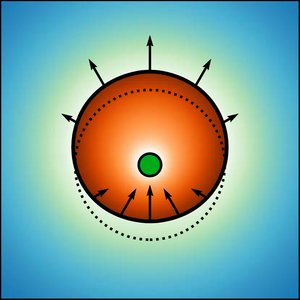
Droplets which form by liquid-liquid phase separation from a solution can provide chemical compartments that localize chemical reactions in space. We consider a simple model of such chemically active droplets in which small colloidal particles are immersed. We show that chemical reactions can lead to a positioning of particles to the geometric center of the droplet. Our work is relevant to the centering of centrioles inside centrosomes of cells.
D. Zwicker, J. Baumgart, S. Redemann, T. Müller-Reichert, A. A. Hyman and F. Jülicher
Phys. Rev. Lett. 121, 158102 (2018)
[PDF (594 kB)]
Differential Lateral and Basal Tension Drive Folding of Drosophila Wing Discs through Two Distinct Mechanisms

We investigate the process by which a flat sheet of cells can undergo a shape change that leads to the formation of a fold in the tissue. Using a combination of experiments and theory we focus on folds that form in the developing fly wing tissue. Our work reveals that a localized reduction of contractile tension on the basal side of the tissue is a key mechanism for fold formation. Furthermore, an increase in lateral contractile tension provides a second mechanism. Our combination of lateral and basal tension estimates with a mechanical tissue model reveals how simple modulations of surface and edge tension drive complex three-dimensional morphological changes.
L. Sui, S. Alt, M. Weigert, N. Dye, S. Eaton, F. Jug, E. W. Myers, F. Jülicher, G. Salbreux and C. Dahmann
Nature Communications 9, 4620 (2018)
[PDF (2,3 MB)]
Role of Hydrodynamic Flows in Chemically Driven Droplet Division
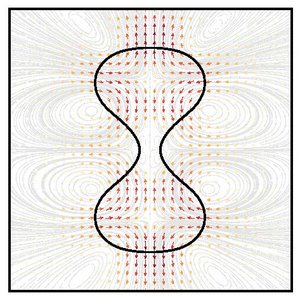
Chemically active droplets provide simple models for protocells. They are maintained away from thermodynamic equilibrium, they take up material, turn over my chemical processes and release reaction products. Most interestingly, they can spontaneously divide and undergo cycles of growth and division. Here, we study the role of hydrodynamic flows for the shape changes and division of chemically active droplets. Our work shows that hydrodynamic flows tends to stabilize spherical shapes and that droplet division occurs for sufficiently strong chemical driving, sufficiently large droplet viscosity or sufficiently small surface tension.
R. Seyboldt and F. Jülicher
New J. Phys. 20, 105010 (2018)
[PDF (1,9 MB)]
Discontinuous switching of position of two coexisting phases
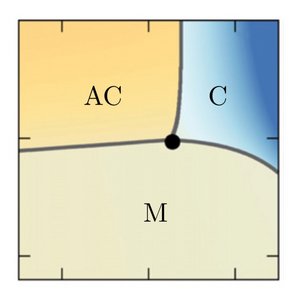
We investigate how the positions of a condensed phase can be controlled by using concentration gradients of a regulator that influences phase separation. We find a novel first order phase transition at which the position of the condensed phase switches in a discontinuous manner. This mechanism could have implications for the spatial organisation of biological cells and provides a control mechanism for droplets in microfluidic systems.
S. Krüger, C. A. Weber, J.-U. Sommer, F. Jülicher
New J. Phys. 20, 075009 (2018)
[PDF (1,2 MB)]
Critical Point in Self-Organized Tissue Growth
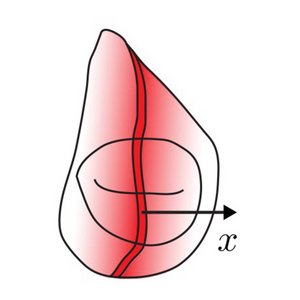
We present a theory of growth control inspired by biological tissues during development. We identify a critical point of the feedback dynamics where a graded profile of a secreted molecule regulates growth. At this critical point, growth is spatially homogeneous and concentration profiles exhibit exact scaling with size. We propose that the observed approximate growth homogeneity and scaling in the fly wing imaginal disk are signatures of this critical point.
D. Aguilar-Hidalgo, S. Werner, O. Wartlick, M. Gonzalez-Gaitan, B. M. Friedrich
and F. Jülicher
Phys. Rev. Lett. 120, 198102 (2018)
[PDF (2,9 MB)]
Chemical event chain model of coupled genetic oscillators
We introduce a stochastic model of coupled genetic oscillators in which chains of chemical events involved in gene regulation and expression are represented as sequences of Poisson processes. We study the quality of noisy oscilations in different parameter regimes. we show that key features of the stochastic oscillations can be captured by an effective model for phase oscillators that are coupled by signals with distributed delays.
D. J. Jörg, L. G. Morelli and F. Jülicher
Phys. Rev. E. 97, 032409 (2018)
[PDF (1,2 MB)]
Generic Properties of Stochastic Entropy Production
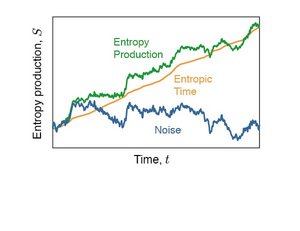
We present a stochastic differential equation for the time evolution of entropy in Langevin processes. We show that entropy fluctuation exhibit universal properties which are a conse-quence of a simple stochastic time transformation.
S. Pigolotti, I. Neri, É. Roldán and F. Jülicher
Phys. Rev. Lett. 119, 140601 (2017)
[PDF (651 kB)]
Mechanics of Active Surfaces
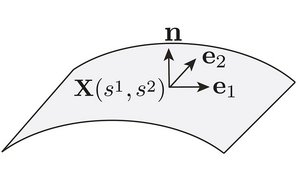
Active matter is driven at molecular scales away from thermodynamic equilibrium by energy transfusing processes. The theory of bulk active matter is well developed and reveals uncon-ventional material properties and the emergence of active stresses. Here we study active matter that is organised in thin films or sheets that are embedded in three dimensional space. We derive a general theory of the mechanics and the material properties of active surfaces that can account for the interplay of active mechanics and surface deformations.
G. Salbreux and F. Jülicher
Phys. Rev. E 96, 032404 (2017)
[PDF (1 MB)]
Last updated: March 31, 2025